题目内容
19.若△ABC外接圆的圆心为O,半径为4,$\overrightarrow{OA}$+2$\overrightarrow{AB}$+2$\overrightarrow{AC}$=0,则$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为( )| A. | 4 | B. | $\sqrt{15}$ | C. | $\sqrt{7}$ | D. | 1 |
分析 首先运用向量的三角形法则,再取取BC的中点D,连接OD并延长到点E,使得$\overrightarrow{DE}$=$\overrightarrow{OD}$,再由向量共线的性质和勾股定理,即可求得向量的投影.
解答 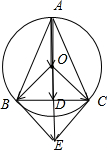 解:如图所示,
解:如图所示,
∵$\overrightarrow{OA}$+2$\overrightarrow{AB}$+2$\overrightarrow{AC}$=$\overrightarrow{0}$,
∴$\overrightarrow{OA}$+2($\overrightarrow{OB}$-$\overrightarrow{OA}$)+2($\overrightarrow{OC}$-$\overrightarrow{OA}$)=$\overrightarrow{0}$,
∴$\overrightarrow{AO}$=$\frac{2}{3}$($\overrightarrow{OB}$+$\overrightarrow{OC}$),
取BC的中点D,连接OD并延长到点E,使得$\overrightarrow{DE}$=$\overrightarrow{OD}$,
则OD⊥BC,$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{OE}$.
∴$\overrightarrow{AO}$=$\frac{2}{3}$$\overrightarrow{OE}$=$\frac{4}{3}$$\overrightarrow{OD}$,
∴|$\overrightarrow{OD}$|=$\frac{3}{4}$|$\overrightarrow{AO}$|=3,
∴CD=$\sqrt{O{C}^{2}-O{D}^{2}}$=$\sqrt{7}$.
∴向量$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为$\sqrt{7}$.
故选C.
点评 本题考查了菱形的性质、向量的平行四边形法则、三角形外心的性质、向量的投影、勾股定理、向量共线定理,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{40}{3}$ | B. | $\frac{16}{3}$ | C. | 8 | D. | 12 |
| A. | y=x2 | B. | y=$\sqrt{x}$ | C. | y=-x3 | D. | y=lg2x |
| A. | q>1 | B. | 0<a1<1 | C. | 0<a6a8<1 | D. | T9<T5 |
| A. | $\frac{7}{5}$ | B. | $\frac{5}{7}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{12}$ |
 如图,三棱锥ABC-A1B1C1的底面ABC是正三角形,A1D⊥平面ABC,D是AC的中点.
如图,三棱锥ABC-A1B1C1的底面ABC是正三角形,A1D⊥平面ABC,D是AC的中点. 如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆. 如图所示,设抛物线y2=2px与圆(x-5)2+y2=16在x轴上方的交点为A和B,线段AB的中点C(4,yC)
如图所示,设抛物线y2=2px与圆(x-5)2+y2=16在x轴上方的交点为A和B,线段AB的中点C(4,yC)