题目内容
 如图四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,设E为BC的中点,二面角P-DE-A为45°.
如图四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,设E为BC的中点,二面角P-DE-A为45°.
(1 ) 求点A到平面PDE的距离;
(2 ) 在PA上确定一点F,使BF∥平面PDE;
(3 ) 求平面PDE与平面PAB所成的不大于直二面角的二面角的大小(用反三角函数表示).
 解:由题意知
解:由题意知(1)∵DE为正△BCD的中线
∴DE⊥BC
∵AD∥BC
∴DE⊥AD,
又∵PA⊥平面ABCD且DE⊆面ABCD
∴DE⊥PD
即∠PDA为二面角P-DE-A的平面角
又∵∠PDA=45°且PA=AD
∴△PAD为等腰直角三角形
作AH⊥PD于H,则DE⊥AH
∴AH⊥平面PDE
又∵PA=AD=2
∴AH=

即点A到平面PDE的距离为
 .
. (2)取PA的中点为F,连接BF,HF
∵F,H分别是PA,PD的中点
∴在△PAD内,HF∥AD且HF=

又∵EB∥AD且EB=

∴EB∥HF且EB=HF
∴四边形FHEB为平行四边形
∴BF∥EH且EH⊆面PDE
∴BF∥平面PDE.
(3)设AB∩DE=M,连PM,作HO⊥PM于O,连AO
∵AH⊥面PDM,且PM⊆面PDM
∴AH⊥PM
又∵HO⊥PM
∴PM⊥面AOH,且AO⊆面AOH
∴PM⊥AO
∴∠AOH为所求二面角的平面角,
∵AO=

∴
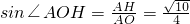
即
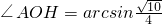
故平面PDE与平面PAB所成的不大于直二面角的二面角的大小
 .
.分析:(1)要想求点到面的距离,必须过点找到底面的垂线,即AH⊥面PDE,那么AH为点A到平面PDE的距离,然后再求线段的长度即可;(2)根据线面平行的判定定理可知,只有在面内找到一条线与已知直线平行,即BF∥EH,线线平行从而达到线面平行的目的;(3)根据定义先作出二面角的平面角,即∠AOH为平面PDE与平面PAB二面角的平面角,然后解三角形即可得到角的大小.
点评:本题主要考查点到面的距离,线面平行的证明及二面角大小的求法,还是有一定的难度.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
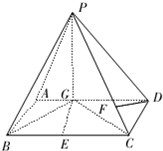 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且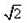 ,F是BC的中点.
,F是BC的中点.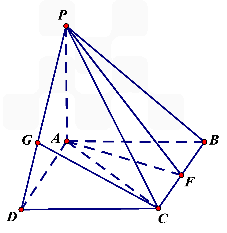
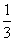 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.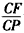 的值。
的值。 
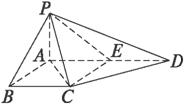
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.