题目内容
(本小题9分)
如图所示,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP,现将 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
(I)求证:PA//平面EFG;
(II)若M为线段CD上的一个动点,问当M在什么位置时,MF与平面EFG所成角最大。
如图所示,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP,现将
 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。(I)求证:PA//平面EFG;
(II)若M为线段CD上的一个动点,问当M在什么位置时,MF与平面EFG所成角最大。

(I)证明见解析。
(II)M 为线段CD中点时,
为线段CD中点时, 最大。
最大。
(II)M
 为线段CD中点时,
为线段CD中点时, 最大。
最大。方法一:
(I)证明: 平面PAD,
平面PAD,
 2分
2分
过P作AD的垂线,垂足为O,则PO 平面ABCD。
平面ABCD。
过O作BC的垂线,交BC于H,以OH,OD,OP为x
轴,y轴,z轴建立空间直角坐标系,
 是二面角P—PC—A的平面角,
是二面角P—PC—A的平面角, ,
,
又
得

故 4分
4分
设平面EFG的一个法向量为 则
则
 6分
6分
而
 故PA//平面EFG。 7分
故PA//平面EFG。 7分
(II)解:设M(x,2,0 ),则
),则 , 9分
, 9分
设MF与平面EFG所成角为 ,
,
则
 12分
12分
故当 取到最大值,则
取到最大值,则 取到最大值,此时点M为线段CD的中点。14分
取到最大值,此时点M为线段CD的中点。14分
方法二:
(I)证明:取AD的中点H,连结EH,HG。 2分
 H,G为AD,BC的中点,∴HG//CD,又EF//CD。
H,G为AD,BC的中点,∴HG//CD,又EF//CD。
∴EF//HG,
∴E,F,G,H四点共面
又∵PA//EH,EH 平面EFGH,PA
平面EFGH,PA 平面EFGH,
平面EFGH,
∴PA//平面EFG。 7分
(II)解:过M作MO⊥平面EFG,垂足O,连结OF,

则 即为MF与平面EFG所成角,因为CD//EF,
即为MF与平面EFG所成角,因为CD//EF,
故CD//平面EFG,故CD上的点M到平面EFG的距离
MO为定长,故要使 最大,只要MF最短,故当
最大,只要MF最短,故当
 时,即M
时,即M 为线段CD中点时,
为线段CD中点时, 最大。
最大。
(I)证明:
 平面PAD,
平面PAD, 2分
2分过P作AD的垂线,垂足为O,则PO
 平面ABCD。
平面ABCD。过O作BC的垂线,交BC于H,以OH,OD,OP为x
轴,y轴,z轴建立空间直角坐标系,
 是二面角P—PC—A的平面角,
是二面角P—PC—A的平面角, ,
,又

得


故
 4分
4分设平面EFG的一个法向量为
 则
则 6分
6分而

 故PA//平面EFG。 7分
故PA//平面EFG。 7分(II)解:设M(x,2,0
 ),则
),则 , 9分
, 9分设MF与平面EFG所成角为
 ,
,则

 12分
12分故当
 取到最大值,则
取到最大值,则 取到最大值,此时点M为线段CD的中点。14分
取到最大值,此时点M为线段CD的中点。14分方法二:
(I)证明:取AD的中点H,连结EH,HG。 2分
 H,G为AD,BC的中点,∴HG//CD,又EF//CD。
H,G为AD,BC的中点,∴HG//CD,又EF//CD。∴EF//HG,
∴E,F,G,H四点共面
又∵PA//EH,EH
 平面EFGH,PA
平面EFGH,PA 平面EFGH,
平面EFGH,∴PA//平面EFG。 7分
(II)解:过M作MO⊥平面EFG,垂足O,连结OF,

则
 即为MF与平面EFG所成角,因为CD//EF,
即为MF与平面EFG所成角,因为CD//EF,故CD//平面EFG,故CD上的点M到平面EFG的距离
MO为定长,故要使
 最大,只要MF最短,故当
最大,只要MF最短,故当 时,即M
时,即M 为线段CD中点时,
为线段CD中点时, 最大。
最大。
练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 与
与 所成的角的余弦值;
所成的角的余弦值;

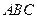
 平面
平面 ,
,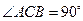 ,
, ,△
,△ 的平面角的正切值为多少.
的平面角的正切值为多少.
 所成的角是 、直线
所成的角是 、直线 和平面
和平面 所成的角为 .
所成的角为 .
 中,
中, ,且
,且 是
是 的中点,点
的中点,点 在
在 上.
上. ;
; 的大小.
的大小. 中,
中, 于
于 ,三边分别是
,三边分别是 ,则有
,则有 ;类比上述结论,写出下列条件下的结论:四面体
;类比上述结论,写出下列条件下的结论:四面体 中,
中, 的面积分别是
的面积分别是 ,二面角
,二面角 的度数分别是
的度数分别是 ,则
,则 .
. 中,
中, ,
, 、
、 分别是
分别是 、
、 的中点,
的中点, ,则异面直线
,则异面直线 、
、 所成的角为 .
所成的角为 . 图2是正方体的展开图,其中直线AB与CD在原正方体中的成角的大小是_______。
图2是正方体的展开图,其中直线AB与CD在原正方体中的成角的大小是_______。