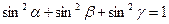题目内容
棱长为2的正方体A1B1C1D1-ABCD中,E、F分别是C1C和D1A1的中点,
(1)求异面直线 与
与 所成的角的余弦值;
所成的角的余弦值;
(2)求点A到EF的距离.
(1)求异面直线
 与
与 所成的角的余弦值;
所成的角的余弦值;(2)求点A到EF的距离.

(1)异面直线 与
与 所成的角的余弦值为
所成的角的余弦值为 ;(2)A到EF的距离为
;(2)A到EF的距离为 .
.
 与
与 所成的角的余弦值为
所成的角的余弦值为 ;(2)A到EF的距离为
;(2)A到EF的距离为 .
.(1)如图,以D为原点,DA、DC、DD1分别为x轴、
y轴、z轴建立空间直角坐标系,则由已知得
A(2,0,0),B(2,2,0),E(0,2,1),F(1,0,2);
∴ =(0,2,0),
=(0,2,0), =(1,
=(1, ,1),
,1), =(1,0,
=(1,0, ),
),
∴ | |=2,|
|=2,| |=
|=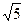 ,
, =
= ;
;
 =
=  ,
,  =
= ,
,
∴ 与
与 夹角的余弦值为cos
夹角的余弦值为cos =
= =
= .
.
∵异面直线所成角的范围是 ,向量的夹角范围是
,向量的夹角范围是 ;
;
∴异面直线 与
与 所成的角的余弦值为
所成的角的余弦值为 .
.
(2)由(1)得 =
= ,|
,| |=
|=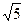 ;
;
∴ 在
在 方向上的射影为
方向上的射影为 =
= ,
,
∴A到EF的距离为 .
.
y轴、z轴建立空间直角坐标系,则由已知得
A(2,0,0),B(2,2,0),E(0,2,1),F(1,0,2);
∴
 =(0,2,0),
=(0,2,0), =(1,
=(1, ,1),
,1), =(1,0,
=(1,0, ),
),∴ |
 |=2,|
|=2,| |=
|=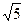 ,
, =
= ;
; =
=  ,
,  =
= ,
,∴
 与
与 夹角的余弦值为cos
夹角的余弦值为cos =
= =
= .
.∵异面直线所成角的范围是
 ,向量的夹角范围是
,向量的夹角范围是 ;
;∴异面直线
 与
与 所成的角的余弦值为
所成的角的余弦值为 .
.(2)由(1)得
 =
= ,|
,| |=
|=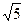 ;
;∴
 在
在 方向上的射影为
方向上的射影为 =
= ,
,∴A到EF的距离为
 .
.
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 是正方形
是正方形 所在平面外一点,
所在平面外一点, 平面
平面 ,点
,点 、
、 分别在线段
分别在线段 、
、 上,满足
上,满足 .
. 与平面
与平面 ;
;
 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
 分别是PB,CD上的点,且
分别是PB,CD上的点,且 ,过点E作BC的平行线交PC于G.
,过点E作BC的平行线交PC于G. 时,求△EFG的面积。
时,求△EFG的面积。
 B.
B. C.
C. D.
D.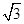
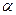 和
和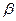 ,则
,则 中,
中, 是等边三角形,
是等边三角形, 面ABC,已知
面ABC,已知 ,
, 在棱
在棱 上,且
上,且 ,则
,则 与平面
与平面 所成的角为( )
所成的角为( )




 ,使直线
,使直线 、
、 ,则
,则 .长方体的一条对角线与三条共顶点的棱所成的角分别为
.长方体的一条对角线与三条共顶点的棱所成的角分别为 ,与三个共顶点的面所成的角分别为
,与三个共顶点的面所成的角分别为 ,用类比推理的方法可知成立的关系式是
,用类比推理的方法可知成立的关系式是