题目内容
一动圆过点A(0,1),圆心在抛物线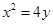 上,且恒与定直线
上,且恒与定直线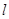 相切,则直线
相切,则直线
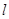 的方程为 。
的方程为 。
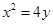 上,且恒与定直线
上,且恒与定直线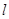 相切,则直线
相切,则直线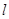 的方程为 。
的方程为 。y=-1
依题意可得,点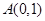 是抛物线
是抛物线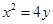 的焦点,设圆心为
的焦点,设圆心为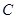 ,根据抛物线的几何性质可知,圆心
,根据抛物线的几何性质可知,圆心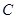 到抛物线准线
到抛物线准线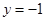 的距离等于圆心
的距离等于圆心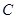 到点
到点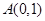 的距离即半径长,所以圆与直线
的距离即半径长,所以圆与直线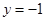 相切,则直线
相切,则直线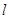 的方程为
的方程为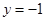
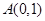 是抛物线
是抛物线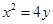 的焦点,设圆心为
的焦点,设圆心为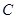 ,根据抛物线的几何性质可知,圆心
,根据抛物线的几何性质可知,圆心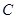 到抛物线准线
到抛物线准线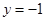 的距离等于圆心
的距离等于圆心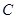 到点
到点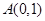 的距离即半径长,所以圆与直线
的距离即半径长,所以圆与直线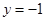 相切,则直线
相切,则直线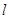 的方程为
的方程为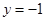

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
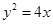 的焦点为圆心,且被
的焦点为圆心,且被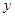 轴截得的弦长等于
轴截得的弦长等于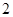 的圆的方程为__________________.
的圆的方程为__________________.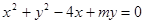 上一点
上一点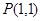 的圆的切线方程为( )
的圆的切线方程为( )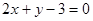
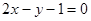

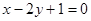
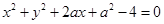 与
与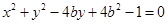 恰有三条公切
恰有三条公切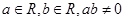 ,则
,则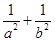 的最小值为( )
的最小值为( )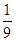
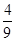
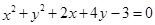 上,且到直线
上,且到直线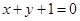 的距离为
的距离为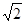 的点共有( )
的点共有( )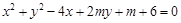 与
与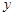 轴的两交点
轴的两交点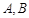 位于原点的同侧,则实数
位于原点的同侧,则实数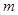

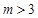 或
或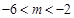
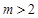 或
或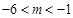
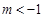
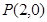 ,及⊙
,及⊙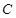 :
: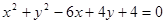 。
。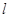 过点
过点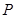 且与圆心
且与圆心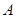 、
、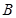 两点,当
两点,当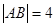 ,求以线段
,求以线段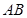 为直径的圆的方程。
为直径的圆的方程。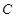 经过两点
经过两点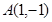 和
和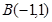 ,且圆心在直线
,且圆心在直线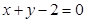 上。
上。