题目内容
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 为等边三角形,
为等边三角形,
![]() 且
且![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
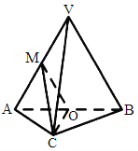
(I)求证:![]() 平面
平面![]() ;
;
(II)求证:平面![]() 平面
平面![]() ;
;
(III)求三棱锥![]() 的体积.
的体积.
【答案】(I)详见解析(II)详见解析(III)![]()
【解析】
试题分析:(Ⅰ)利用三角形的中位线得出OM∥VB,利用线面平行的判定定理证明VB∥平面MOC;(Ⅱ)证明OC⊥平面VAB,即可证明平面MOC⊥平面VAB;(Ⅲ)利用等体积法求三棱锥A-MOC的体积即可
试题解析:(Ⅰ)证明:∵O,M分别为AB,VA的中点,
∴OM∥VB,
∵VB平面MOC,OM平面MOC,
∴VB∥平面MOC;
(Ⅱ)证明:∵AC=BC,O为AB的中点,
∴OC⊥AB,
又∵平面VAB⊥平面ABC,平面ABC∩平面VAB=AB,且OC平面ABC,
∴OC⊥平面VAB,
∵OC平面MOC,
∴平面MOC⊥平面VAB
(Ⅲ)在等腰直角三角形![]() 中,
中,![]() ,
,
所以![]() .
.
所以等边三角形![]() 的面积
的面积![]() .
.
又因为![]() 平面
平面![]() ,
,
所以三棱锥![]() 的体积等于
的体积等于![]() .
.
又因为三棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积相等,
的体积相等,
所以三棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
相关题目
【题目】重庆八中大学城校区与本部校区之间的驾车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
| 25 | 30 | 35 | 40 |
频数(次) | 100 | 150 | 200 | 50 |
以这500次驾车单程所需时间的频率代替某人1次驾车单程所需时间的概率.
(1)求![]() 的分布列与
的分布列与![]() ;
;
(2)某天有3位教师独自驾车从大学城校区返回本部校区,记![]() 表示这3位教师中驾车所用时间少于
表示这3位教师中驾车所用时间少于![]() 的人数,求
的人数,求![]() 的分布列与
的分布列与![]() ;
;
(3)下周某天张老师将驾车从大学城校区出发,前往本部校区做一个50分钟的讲座,结束后立即返回大学城校区,求张老师从离开大学城校区到返回大学城校区共用时间不超过120分钟的概率.