题目内容
本小题满分10分
已知二次函数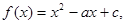
（其中
）.
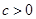(1)若函数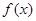
为偶函数，求
的值；
(2)当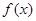为偶函数时，若函数
，指出
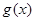在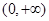
上单调性情况，并证明之.
（1）
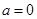；（2）见解析。
解析
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
本小题满分10分
已知二次函数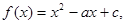（其中）.
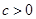(1)若函数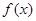为偶函数，求的值；
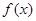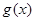(2)当为偶函数时，若函数，指出在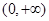上单调性情况，并证明之.
（1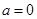） ；（2）见解析。
解析
天天向上一本好卷系列答案小学生10分钟应用题系列答案
的解集为
，不等式
的解集为
。
； 
的解集为
的解集。
（
为实数，
，
），若
，且函数
的值域为
． 
时，
是单调函数，求实数
的取值范围．
（阴影部分）和环公园人行道组成.已知休闲区
m ，求公园ABCD所占面积
关于 x 的函数
的解析式；
；
且
，求
的值.
.
的定义域和值域均是
，求实数
的值；
上是减函数，且对任意的
，总有
，求实数
在
上有定义，对任意实数
和任意实数
，都有
. 
；
（其中k和h均为常数）；
的时，设
，讨论
在
内的单调性.
满足，
时，
。
时，
上递减。 
是
上的偶函数．
的值;
,若函数
与
的图象有且只有一个公共点,求实数
的取值范围．