题目内容
已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax2+2bx+c=0，bx2+2cx+a=0，cx2+2ax+b=0至少有一个方程有两个相异实根，应假设成（ ）
| A．三个方程都没有两个相异实根 | B．一个方程没有两个相异实根 |
| C．至多两个方程没有两个相异实根 | D．三个方程不都没有两个相异实根 |
A
略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
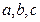的倒数成等差数列，求证：角
.
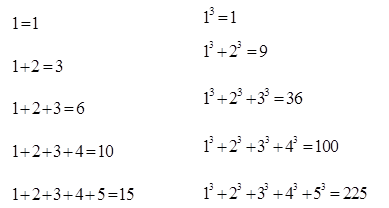
(用含有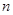
的式子表示，其中
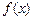在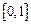
上有意义,且
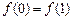,如果对于不同的
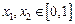,都有
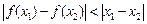，求证：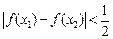
。那么他的反设应该是___________．
”，应假设为_____________ ．
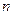为正整数，用数学归纳法证明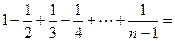
时，若已假设
（
为偶数）真，则还需利用归纳假设再证（ ）
时等式也成立 B
、
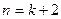时等式也成立 
时等式也成立 D、
时等式也成立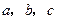
都是偶数”，正确的反设为（***）