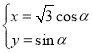ƒøƒ⁄»ð
°æƒø°øƒ≥“Ω—ß‘∫”˚—–æø÷Á“πŒ¬≤Ó¥Û–°”Ϊº∏–√∞»À ˝∂ý…Ÿ÷ƺ‰µƒπÿœµ£¨∏√‘∫≈…≥ˆ—–æø–°◊È∑÷±µΩ∆¯œÛæ÷”΃≥“Ω‘∫£¨≥≠¬º¡À1µΩ6‘¬∑ð√ø‘¬10∫≈µƒ÷Á“πŒ¬≤Ó«Èøˆ”Γڪº∏–√∞∂¯æÕ’Ôµƒ»À ˝£¨µ√µΩ ˝æð◊ ¡œº˚±Ì£∫
‘¬∑ð | 1 | 2 | 3 | 4 | 5 | 6 |
÷Á“πŒ¬≤Ó£®°Ê£© | 10 | 11 | 13 | 12 | 8 | 6 |
æÕ’Ô»À ˝£®∏ˆ£© | 23 | 26 | 30 | 27 | 17 | 13 |
∏√—–æø–°◊È»∑∂®µƒ—–æø∑Ω∞∏ «£∫œ»¥”’‚¡˘◊È ˝æð÷–—°»°2◊È£¨”√ £œ¬µƒ4◊È ˝æð«Ûœþ–‘ªÿπÈ∑Ω≥㨑Ÿ”√±ª—°»°µƒ2◊È ˝æðΩ¯––ºÏ—È£Æ
£®1£©«Û—°»°µƒ2◊È ˝æð«°∫√ «œý¡⁄µƒ¡Ω∏ˆ‘¬µƒ∏≈¬ £ª
£®2£©“—÷™—°»°µƒ «1‘¬”Î6‘¬µƒ¡Ω◊È ˝æð£Æ
£®i£©«Î∏˘æð2µΩ5‘¬∑𵃠˝æ𣨫ÛæÕ’Ô»À ˝yπÿ”⁄÷Á“πŒ¬≤Óxµƒœþ–‘ªÿπÈ∑Ω≥ã∫
£®ii£©»Ù”…œþ–‘ªÿπÈ∑Ω≥õ√µΩµƒπ¿º∆ ˝æð”ÎÀ˘—°≥ˆµƒºÏ—È ˝æ𵃌Û≤Óæ˘≤ª≥¨π˝2»À£¨‘Ú»œŒ™µ√µΩµƒœþ–‘ªÿπÈ∑Ω≥à «¿ÌœÎµƒ£¨ ‘Œ ∏√—–æø–°◊ÈÀ˘µ√µƒœþ–‘ªÿπÈ∑Ω≥à «∑ҿ̜Σø
£®≤Œøºπ´ Ω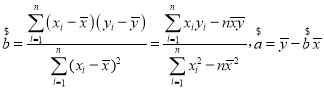 £©
£©
°æ¥∞∏°ø£®1£©![]() £®2£©£®i£©y
£®2£©£®i£©y![]() £®ii£©∏√–°◊ÈÀ˘µ√œþ–‘ªÿπÈ∑Ω≥à «¿ÌœÎµƒ£Æ
£®ii£©∏√–°◊ÈÀ˘µ√œþ–‘ªÿπÈ∑Ω≥à «¿ÌœÎµƒ£Æ
°æΩ‚Œˆ°ø
£®1£©‘À”√¡–æŸ∑®”Îπ≈µ‰∏≈–Õπ´ Ω«ÛΩ‚£ª
£®2£©£®i£©«Û≥ˆ![]() £¨¥˙»Îπ´ Ω«Ûµ√
£¨¥˙»Îπ´ Ω«Ûµ√![]() £¨º¥ø…µ√œþ–‘ªÿπÈ∑Ω≥㪣®ii£©ΩË÷˙”ΪÿπÈ∑Ω≥Ã∑÷ŒˆÃΩæøº¥ø….
£¨º¥ø…µ√œþ–‘ªÿπÈ∑Ω≥㪣®ii£©ΩË÷˙”ΪÿπÈ∑Ω≥Ã∑÷ŒˆÃΩæøº¥ø….
£®1£©…Ë—°»°µƒ2◊È ˝æð«°∫√ «œý¡⁄¡Ω∏ˆ‘¬Œ™ ¬º˛A£¨
“ÚŒ™¥”6◊È ˝æð÷–—°»°2◊È ˝æðπ≤”–15÷÷«Èøˆ£¨
![]() £¨√ø÷÷«Èøˆ∂º «µ»ø…ƒÐ≥ˆœ÷µƒ£¨
£¨√ø÷÷«Èøˆ∂º «µ»ø…ƒÐ≥ˆœ÷µƒ£¨
∆‰÷–—°»°µƒ2◊È ˝æð«°∫√ «œý¡⁄¡Ω∏ˆ‘¬µƒ«Èøˆ”–5÷÷£¨
À˘“‘![]() £¨
£¨
£®2£©![]() £¨
£¨![]() £¨
£¨
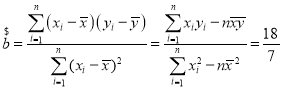 £¨
£¨
![]()
![]() £¨
£¨
µ√µΩyπÿ”⁄xµƒªÿπÈ÷±œþ∑Ω≥ÃŒ™y![]() .
.
£®2£©µ±x£Ω10 ±£¨y![]() £¨
£¨![]() £¨
£¨
Õ¨—˘£¨µ±x£Ω6 ±£¨y![]() £¨
£¨![]() £¨
£¨
π¿º∆ ˝æð”ÎÀ˘—°≥ˆµƒºÏ—È ˝æ𵃌Û≤Óæ˘≤ª≥¨π˝2»À£¨
°ý∏√–°◊ÈÀ˘µ√œþ–‘ªÿπÈ∑Ω≥à «¿ÌœÎµƒ£Æ

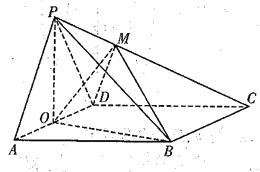
°æƒø°øƒ≥Õ¨—ß”√°∞Àʪ˙ƒ£ƒ‚∑Ω∑®°±º∆À„«˙œþ![]() ”Î÷±œþ
”Î÷±œþ![]() À˘Œß≥…µƒ«˙±þ»˝Ω«–Œµƒ√ʪ˝ ±£¨”√º∆À„ª˙∑÷±≤˙…˙¡À10∏ˆ‘⁄«¯º‰[1£¨e]…œµƒæ˘‘»Àʪ˙ ˝xi∫Õ10∏ˆ‘⁄«¯º‰[0£¨1]…œµƒæ˘‘»Àʪ˙ ˝
À˘Œß≥…µƒ«˙±þ»˝Ω«–Œµƒ√ʪ˝ ±£¨”√º∆À„ª˙∑÷±≤˙…˙¡À10∏ˆ‘⁄«¯º‰[1£¨e]…œµƒæ˘‘»Àʪ˙ ˝xi∫Õ10∏ˆ‘⁄«¯º‰[0£¨1]…œµƒæ˘‘»Àʪ˙ ˝![]()
![]() £¨∆‰ ˝æð»Áœ¬±Ìµƒ«∞¡Ω––£Æ
£¨∆‰ ˝æð»Áœ¬±Ìµƒ«∞¡Ω––£Æ
x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
lnx | 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
”…¥Àø…µ√’‚∏ˆ«˙±þ»˝Ω«–Œ√ʪ˝µƒ“ª∏ˆΩ¸À∆÷µŒ™£® £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
°æƒø°øƒ≥µÿ«¯»À√Ò∑®‘∫√øƒÍ“™…Û¿Ì¥Û¡ø∞∏º˛£¨»•ƒÍ…ۿ̵ƒÀƒ¿ý∞∏º˛«Èøˆ»Á±ÌÀ˘ æ£∫
±ý∫≈ | œÓƒø | ’∞∏£®º˛£© | Ω·∞∏£®º˛£© | |
≈–戣®º˛£© | ||||
1 | –à ¬∞∏º˛ | 2400 | 2400 | 2400 |
2 | ªÈ“ˆº“Õ•°¢ºÃ≥–æ¿∑◊∞∏º˛ | 3000 | 2900 | 1200 |
3 | »® Ù°¢«÷»®æ¿∑◊∞∏º˛ | 4100 | 4000 | 2000 |
4 | ∫œÕ¨æ¿∑◊∞∏º˛ | 14000 | 13000 | n |
∆‰÷–Ω·∞∏∞¸¿®£∫∑®Õ•µ˜Ω‚∞∏º˛°¢≥∑Àþ∞∏º˛°¢≈–æˆ∞∏º˛µ»£Æ∏˘æð“‘…œ ˝æ𣨪ÿ¥œ¬¡–Œ £Æ
£®¢Ò£©‘⁄±ý∫≈Œ™1°¢2°¢3µƒ ’∞∏∞∏º˛÷–Àʪ˙»°1º˛£¨«Û∏√º˛ «Ω·∞∏∞∏º˛µƒ∏≈¬ £ª
£®¢Ú£©‘⁄±ý∫≈Œ™2µƒΩ·∞∏∞∏º˛÷–Àʪ˙»°1º˛£¨«Û∏√º˛ «≈–æˆ∞∏º˛µƒ∏≈¬ £ª
£®¢Û£©‘⁄±ý∫≈Œ™1°¢2°¢3µƒ»˝¿ý∞∏º˛÷–£¨≈–æˆ∞∏º˛ ˝µƒ∆Ωæ˘ ˝Œ™![]() £¨∑Ω≤ÓŒ™S12£¨»Áπ˚±Ì÷–n
£¨∑Ω≤ÓŒ™S12£¨»Áπ˚±Ì÷–n![]() £¨±Ì÷–»´≤ø£®4¿ý£©∞∏º˛µƒ≈–æˆ∞∏º˛ ˝µƒ∑Ω≤ÓŒ™S22£¨ ‘≈–∂œS12”ÎS22µƒ¥Û–°πÿœµ£¨≤¢–¥≥ˆƒ„µƒΩ·¬€£®Ω·¬€≤ª“™«Û÷§√˜£©£Æ
£¨±Ì÷–»´≤ø£®4¿ý£©∞∏º˛µƒ≈–æˆ∞∏º˛ ˝µƒ∑Ω≤ÓŒ™S22£¨ ‘≈–∂œS12”ÎS22µƒ¥Û–°πÿœµ£¨≤¢–¥≥ˆƒ„µƒΩ·¬€£®Ω·¬€≤ª“™«Û÷§√˜£©£Æ