题目内容
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.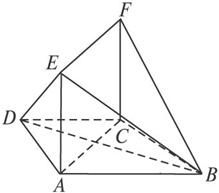
(1)求证:BC⊥平面ACFE;
(2)当EM为何值时,AM∥平面BDF?证明你的结论.
解:(1)在梯形ABCD中,∵AB∥CD,AD=DC=CB=a,∠ABC=60°,∴四边形ABCD是等腰梯形,且∠DCA=∠DAC=30°,∠DCB=120°.∴∠ACB=90°.∴AC⊥BC.又∵平面ACFE⊥面ABCD,交线为AC,∴BC⊥平面ACFE.
(2)当EM=![]() a时,AM∥平面BDF.
a时,AM∥平面BDF.
在梯形ABCD中,设AC∩BD=N,连结FN,则CN∶NA=1∶2.∵EM=![]() a,而EF=AC=
a,而EF=AC=![]() a,
a,
∴EM∶MF=1∶2.∴MF∥AN.∴四边形ANFM是平行四边形.∴AM∥NF.又∵NF![]() 平面BDF,AM
平面BDF,AM![]() 平面BDF,∴AM∥平面BDF.
平面BDF,∴AM∥平面BDF.

练习册系列答案
相关题目
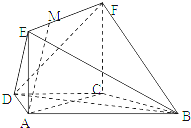 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.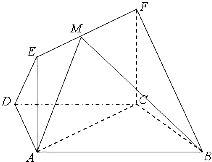 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.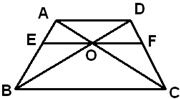 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.