题目内容
20．如图，网格纸上正方形小格的边长为1，图中粗线画出的是某零件的三视图，则该零件的表面积为（ ）
| A． | 37π | B． | 46π | C． | 50π | D． | 54π |
分析 由三视图判断几何体的形状，通过三视图的数据求解几何体的各面面积，累加可得答案．
解答 解：几何体是由两个圆柱组成，一个是底面半径为3高为2，
一个是底面半径为2，高为4，
其表面相当于底面半径为3高为2圆柱表面积与底面半径为2，高为4圆柱侧面积之和，
底面半径为3高为2圆柱表面积为2π×3×（3+2）=30π，
底面半径为2，高为4圆柱侧面积为：2π×2×4=16π，
故组合体的表面积S=30π+16π=46π，
故选：B
点评 本题考查的知识点是由三视图求体积和表面积，其中根据已知分析出几何体的形状，是解答的关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
12．设等差数列{an}的前n项和为Sn，且满足S20＞0，S21＜0，则$\frac{S_1}{a_1}，\frac{S_2}{a_2}，…，\frac{{{S_{21}}}}{{{a_{21}}}}$中最大的项为（ ）
| A． | $\frac{s_8}{a_8}$ | B． | $\frac{{{s_{10}}}}{{{a_{10}}}}$ | C． | $\frac{{{s_{11}}}}{{{a_{11}}}}$ | D． | $\frac{{S}_{9}}{{a}_{9}}$ |
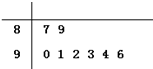某校高二年级8个班参加合唱比赛的得分如面茎叶图所示，则这组数据的中位数和平均数为91.5和91.5．