题目内容
设F1,F2为椭圆 +y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P,Q两点,当四边形PF1QF2的面积最大时,
+y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P,Q两点,当四边形PF1QF2的面积最大时, ·
· 的值等于( )
的值等于( )
 +y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P,Q两点,当四边形PF1QF2的面积最大时,
+y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P,Q两点,当四边形PF1QF2的面积最大时, ·
· 的值等于( )
的值等于( )| A.0 | B.2 | C.4 | D.-2 |
D
【思路点拨】数形结合利用几何法求解.
易知当P,Q分别在椭圆短轴端点时,四边形PF1QF2的面积最大,
此时F1(- ,0),F2(
,0),F2( ,0),不妨设P(0,1),
,0),不妨设P(0,1),
∴ =(-
=(- ,-1),
,-1), =(
=( ,-1),
,-1),
∴ ·
· =-2.
=-2.
易知当P,Q分别在椭圆短轴端点时,四边形PF1QF2的面积最大,
此时F1(-
 ,0),F2(
,0),F2( ,0),不妨设P(0,1),
,0),不妨设P(0,1),∴
 =(-
=(- ,-1),
,-1), =(
=( ,-1),
,-1),∴
 ·
· =-2.
=-2.
练习册系列答案
相关题目
 +
+ =1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2:
=1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2: ,
, ),Q(
),Q( ,1),求椭圆C1的方程;
,1),求椭圆C1的方程; 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上且过点
轴上且过点 ,离心率是
,离心率是 .
. 的标准方程;
的标准方程; 且与椭圆
且与椭圆 ,
, 两点,若
两点,若 ,求直线的方程.
,求直线的方程.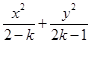 =1表示焦点在y轴上的椭圆,则实数k的取值范围是( )
=1表示焦点在y轴上的椭圆,则实数k的取值范围是( )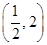
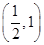
 =1的交点为A,B,点P是椭圆上的动点,则使得△PAB的面积为
=1的交点为A,B,点P是椭圆上的动点,则使得△PAB的面积为 的点P的个数为 .
的点P的个数为 . +
+ =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )



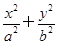 =1(a>b>0)的两个焦点分别为F1,F2,离心率为
=1(a>b>0)的两个焦点分别为F1,F2,离心率为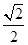 ,且过点(2,
,且过点(2,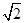 ).
).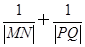 为定值.
为定值.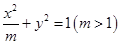 和双曲线
和双曲线 有相同的焦点
有相同的焦点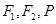 是它们的一个交点,则
是它们的一个交点,则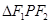 的形状是( )
的形状是( )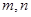 的变化而变化
的变化而变化