题目内容
直线y=x+m与曲线y=
有两个交点,则实数m的取值范围是______.
| 1-2x2 |
由题意可得曲线y=
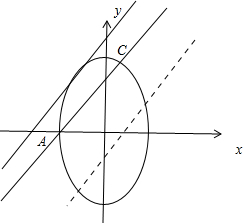
表示焦点在y轴上的椭圆y2+2x2=1的上半部分
联立方程
可得3x2+2mx+m2-1=0
△=4m2-12(m2-1)=0时,m=
或m=-
结合图形可知,当m=
时,直线y=x+m与椭圆y2+2x2=1的上半部分相切
当直线y=x+m过A(-
,0)时,直线y=x+m与椭圆y2+2x2=1的上半部分有2个交点,此时m=
所以,
≤m<
故答案为:[
,
)
| 1-2x2 |
联立方程
|
△=4m2-12(m2-1)=0时,m=
| ||
| 2 |
| ||
| 2 |
结合图形可知,当m=
| ||
| 2 |
当直线y=x+m过A(-
| ||
| 2 |
| ||
| 2 |
所以,
| ||
| 2 |
| ||
| 2 |
故答案为:[
| ||
| 2 |
| ||
| 2 |


练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目