题目内容
如图,在正三棱柱ABC-A1B1C1中,E∈BB1,截面A1EC⊥侧面AC1.
(Ⅰ)求证:BE=EB1;
(Ⅱ)若AA1=A1B1;求平面A1EC与平面A1B1C1所成二面角(锐角)的度数.
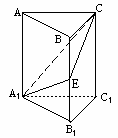
注意:在下面横线上填写适当内容,使之成为(Ⅰ)的完整证明,并解答(Ⅱ).
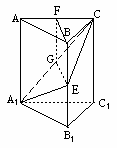
(Ⅰ)证明:在截面A1EC内,过E作EG⊥A1C,G是垂足.
① ∵
∴EG⊥侧面AC1;取AC的中点F,连结BF,FG,由AB=BC得BF⊥AC,
② ∵
∴BF⊥侧面AC1;得BF∥EG,BF、EG确定一个平面,交侧面AC1于FG.
③ ∵
∴BE∥FG,四边形BEGF是平行四边形,BE=FG,
④ ∵
∴FG∥AA1,△AA1C∽△FGC,
⑤ ∵
![]() 即
即![]() ,故
,故![]()
解 (Ⅰ)①∵面A1EC⊥侧面AC1, ②∵面ABC⊥侧面AC1, ③∵BE∥侧面AC1, ④∵BE∥AA1, ⑤∵AF=FC, 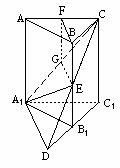
(Ⅱ)解:分别延长CE、C1B1交于点D,连结A1D.
∵![]()
∴![]()
∵![]()
![]()
∴![]() 即
即![]()
∵CC1⊥面A1C1B1,即A1C1是A1C在平面A1C1D上的射影,根据三垂线定理得DA1⊥A1C,
所以∠CA1C1所求二面角的平面角. ∵CC1=AA1=A1B1=A1C1,∠A1C1C=90°,
∴∠CA1C1=45°,即所求二面角为45°.

 名校课堂系列答案
名校课堂系列答案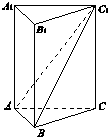 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
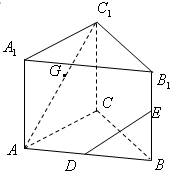 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.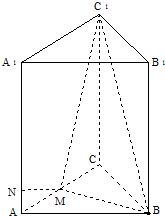 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,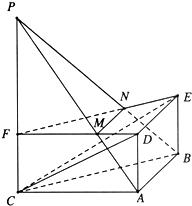 (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.