题目内容
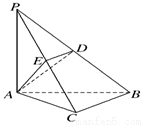
(本小题满分14分).如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC的中点,且DE∥BC.
(1)求证:DE∥平面ACD
(2)求证:BC⊥平面PAC;
(3)求AD与平面PAC所成的角的正弦值;
【答案】
(1)略 ;(2)见解析;(3) AD与平面PAC所成角的正弦值为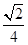 .
.
【解析】本题考查直线与平面垂直的判定,直线与平面所成的角,考查逻辑思维能力,空间想象能力,是中档题.
(1)因为DE∥BC.可以推理证明DE∥平面ACD
(2)要证BC⊥平面PAC,只需证明BC垂直平面PAC内的两条相交直线PA、AC即可;
(3)D为PB的中点,作出AD与平面PAC所成的角∠DAE,然后求其余弦值即可
解:(1)略 。。。。。。。。4分
(2)∵PA⊥底面ABC,∴PA⊥BC.
又∠BCA=90°,∴AC⊥BC,∴BC⊥平面PAC. 。。。。。。。。。9分
(3)∵D为PB的中点,DE∥BC, ∴DE=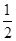 BC.
BC.
又由(1)知,BC⊥平面PAC, ∴DE⊥平面PAC,垂足为点E,
∴∠DAE是AD与平面PAC所成的角.。。。。。。。。。。。。。。。。。。11分
∵PA⊥底面ABC,∴PA⊥AB.
又PA=AB,∴△ABP为等腰直角三角形,∴AD=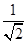 AB.
AB.
在Rt△ABC中,∠ABC=60°,∴BC=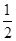 AB,
AB,
∴在Rt△ADE中,sin∠DAE=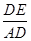 =
=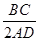 =
=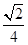 ,
,
即AD与平面PAC所成角的正弦值为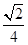 .。。。。。。。。。。。。。。。。14分
.。。。。。。。。。。。。。。。。14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)