题目内容
4.在边长为2的正方形ABCD中,E为CD的中点,F在边BC上,若$\overrightarrow{AD}$•$\overrightarrow{AF}$=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=0.分析 以AB 所在的直线为x轴,以AD所在的直线为y轴,建立直角坐标系,可得A、B、C、D、E点的坐标,设 F (2,b),由$\overrightarrow{AD}$•$\overrightarrow{AF}$=2,故b的值,可得F的坐标,从而求得$\overrightarrow{AF}$•$\overrightarrow{BE}$的值.
解答 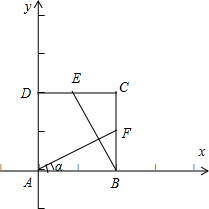 解:如图所示:以AB 所在的直线为x轴,以AD所在的直线为y轴,建立直角坐标系,
解:如图所示:以AB 所在的直线为x轴,以AD所在的直线为y轴,建立直角坐标系,
则由题意可得A (0,0)、B(2,0)、C(2,2)、D(0,2)、E(1,2),
设 F (2,b).
由于$\overrightarrow{AD}$•$\overrightarrow{AF}$=(0,2)•(2,b)=2b=2,故b=1,故F(2,1),$\overrightarrow{BE}$=(-1,2),
则$\overrightarrow{AF}$•$\overrightarrow{BE}$=(2,1)•(-1,2)=-2+2=0,
故答案为:0.
点评 本题主要考查两个向量坐标形式的运算,两个向量的数量积公式的应用,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
14.在空间直角坐标系Oxyz中,点A(-3,-4,5)关于平面xOz的对称点的坐标为( )
| A. | (3,-4,5) | B. | (-3,-4,-5) | C. | (3,-4,-5) | D. | (-3,4,5) |
15.已知集合A={-1,0,1,2},B={x|1≤2x<4},则A∩B=( )
| A. | {-1,0,1} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
12.若直线ax+(2a-3)y=0的倾斜角为45°,则a等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
19.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}\right.$,则目标函数z=$\frac{y+1}{x+1}$的最大值为( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{6}{5}$ | D. | $\frac{2}{3}$ |
9.从双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若M为线段FP的中点,O为坐标原点,则|MO|-|MT|与b-a的大小关系为( )
| A. | |MO|-|MT|>b-a | B. | |MO|-|MT|=b-a | C. | |MP|-|MT|<b-a | D. | 不确定 |
16.抛物线y2=2px的准线方程为x=-1,则p=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
13. 如图,正方体ABCD-A1B1C1D1的棱长为2$\sqrt{3}$,以顶点A为球心,4为半径作一个球,则图中球面与正方体的表面相交所得的两段弧长之和等于( )
如图,正方体ABCD-A1B1C1D1的棱长为2$\sqrt{3}$,以顶点A为球心,4为半径作一个球,则图中球面与正方体的表面相交所得的两段弧长之和等于( )
 如图,正方体ABCD-A1B1C1D1的棱长为2$\sqrt{3}$,以顶点A为球心,4为半径作一个球,则图中球面与正方体的表面相交所得的两段弧长之和等于( )
如图,正方体ABCD-A1B1C1D1的棱长为2$\sqrt{3}$,以顶点A为球心,4为半径作一个球,则图中球面与正方体的表面相交所得的两段弧长之和等于( )| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{7π}{6}$ |