题目内容
2.长江两岸之间没有大桥的地方,常常通过轮渡进行运输,如图所示,一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.(1)试用向量表示江水速度、船速以及船实际航行的速度
(2)求船实际航行的速度的大小(保留两个有效数字)与方向(用与江水速度间的夹角表示,精确到度)
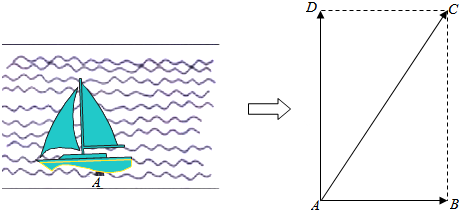
分析 (1)$\overrightarrow{AD}$表示船速,$\overrightarrow{AB}$表示水速,以AD、AB为邻边作平行四边形ABCD,则$\overrightarrow{AC}$表示船实际航行的速度.
(2)利用勾股定理,结合三角函数,即可得出结论.
解答 解:(1)如上图所示.$\overrightarrow{AD}$表示船速,$\overrightarrow{AB}$表示水速,以AD、AB为邻边作平行四边形ABCD,则$\overrightarrow{AC}$表示船实际航行的速度.
(2)在Rt△ABC中,|$\overrightarrow{AB}$|=2,|$\overrightarrow{BC}$|=5,
∴|$\overrightarrow{AC}$|=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$≈5.4.
∵tan∠CAB=2.5,
由计算器得∠CAB≈70°.
答:船实际航行速度的大小约为5.4 km/h,方向与水的流速间的夹角约为70°.
点评 本题用向量知识解决物理问题.由于速度是矢量,可以用向量表示速度,然后用向量加法运算合成速度即可.但要注意解决实际问题中的向量问题不仅要求出大小,而且要求出方向.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.函数y=x3-lnx在x=1处的切线方程为( )
| A. | 2x+y-1=0 | B. | 2x+y+1=0 | C. | 2x-y-1=0 | D. | 2x-y+1=0 |