题目内容
17.下列说法正确的是( )| A. | “若a>1,a2>1”的否命题是“若a>1,a2≤1” | |
| B. | {an}为等比数列,则“a1<a2<a3”是“a4<a5”的既不充分也不必要条件 | |
| C. | ?x0∈(-∞,0),使${3^{x_0}}<{4^{x_0}}$成立 | |
| D. | “若$tanα≠\sqrt{3}$,则$α≠\frac{π}{3}$”是真命题 |
分析 A.利用否命题的定义即可判断出;
B.设等比数列{an}的公比为q,由a1<a2<a3,则${a}_{1}<{a}_{1}q<{a}_{1}{q}^{2}$,若a1<0,则1>q>0,此时a4-a5<0;若a1>0,则q>1.此时a4-a5<0,反之也成立,因即可判断出正误.
C.不?x0∈(-∞,0),使${3^{x_0}}<{4^{x_0}}$成立;
D.其逆否命题为:“若$α=\frac{π}{3}$,则$tanα=\sqrt{3}$”是真命题,即可判断出原命题的真假.
解答  解:A.“若a>1,a2>1”的否命题是“若a≤1,a2≤1”,因此不正确;
解:A.“若a>1,a2>1”的否命题是“若a≤1,a2≤1”,因此不正确;
B.设等比数列{an}的公比为q,由a1<a2<a3,则${a}_{1}<{a}_{1}q<{a}_{1}{q}^{2}$,若a1<0,则1>q>0,此时a4-a5=${a}_{1}{q}^{3}(1-q)$<0,∴a4<a5;若a1>0,则q>1.此时a4-a5=${a}_{1}{q}^{3}(1-q)$<0,∴a4<a5.反之也成立,
因此{an}为等比数列,则“a1<a2<a3”是“a4<a5”的充要条件.因此不正确.
C.不?x0∈(-∞,0),使${3^{x_0}}<{4^{x_0}}$成立,不正确;
D.“若$tanα≠\sqrt{3}$,则$α≠\frac{π}{3}$”,其逆否命题为:“若$α=\frac{π}{3}$,则$tanα=\sqrt{3}$”是真命题,因此原命题是真命题.
故选:D.
点评 本题考查了简易逻辑的判定方法、数列的单调性、指数函数的单调性、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.若函数y=logax的图象过点($\frac{1}{4}$,-2),则底a=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
5.已知数列{an}中,a1=1,an=n(an+1-an)(n∈N*),则数列{an}的通项公式为( )
| A. | 2n-1 | B. | n | C. | ${(\frac{n+1}{n})^{n-1}}$ | D. | n2 |
12.某学校安排3位老师与5名学生去3地参观学习,每地至少去1名老师和1名学生,则不同的安排方法总数为( )
| A. | 1800 | B. | 900 | C. | 300 | D. | 1440 |
2.△ABC中,角A,B,C所对边的边长分别为a,b,c,若$\frac{cosA}{cosB}$=$\frac{a}{b}$,则△ABC一定是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
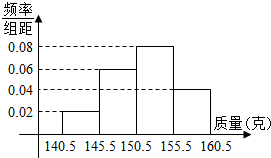 为了了解某种进口茶叶的质量(单位:克),从中抽取若干包进行检查,获得样本的频率分布直方图如图所示.若已知样本中质量在[155.5,160.5)内的茶叶有10包,则样本容量为( )
为了了解某种进口茶叶的质量(单位:克),从中抽取若干包进行检查,获得样本的频率分布直方图如图所示.若已知样本中质量在[155.5,160.5)内的茶叶有10包,则样本容量为( )