求证:正方体ABCD-A1B1C1D1中.对角线B1D与平面A1BC1互相垂直．题目和参考答案——青夏教育精英家教网——

题目内容

19．

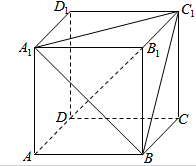求证：正方体ABCD-A₁B₁C₁D₁中，对角线B₁D与平面A₁BC₁互相垂直．

分析连接B₁D₁，则证明A₁C₁⊥B₁D，由此可证BC₁⊥B₁D即可证明B₁D⊥平面A₁C₁B．

解答证明：如图示：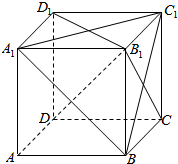
，
连接B₁D₁，则B₁D₁⊥A₁C₁，
∵BB₁⊥A₁C₁，
∴A₁C₁⊥平面BB₁D₁D，
∵B₁D?平面BB₁DD₁，
∴A₁C₁⊥B₁D，
∵由（2）可证BC₁⊥B₁D；BC₁∩A₁C₁=C₁，
∴B₁D⊥平面A₁C₁B，得证．

点评本题主要考查了直线与平面垂直的判定，考查直线和平面所成的角，求直线和平面所成的角关键是找到斜线在平面内的射影，把空间角转化为平面角求解，属基本知识的考查．

练习册系列答案

寒假作业本大象出版社系列答案

寒假作业江西教育出版社系列答案

愉快的寒假南京出版社系列答案

优化学习寒假20天系列答案

优等生快乐寒假云南人民出版社系列答案

优等生寒假作业云南人民出版社系列答案

赢在假期抢分计划寒假合肥工业大学出版社系列答案

赢在假期期末加寒假合肥工业大学出版社系列答案

赢在寒假期末冲刺王云南科技出版社系列答案

本土教辅赢在寒假高效假期总复习云南科技出版社系列答案

相关题目

9．已知$\overrightarrow{a}$=（3，4），$\overrightarrow{b}$=（-6，-8），求cos＜$\overrightarrow{a}$•$\overrightarrow{b}$＞．

10．已知点A（-2，1），B（3，-1）关于直线l对称，且点（2，$\frac{3}{2}$）在直线l上，则直线l的方程是2x-2y-1=0．

7．已知函数f（x）=sin²（x-$\frac{π}{3}$）+2acos（x+$\frac{π}{6}$）．
（1）若a=1，且α是第三象限角，f（α）=-$\frac{5}{9}$，求tan（α-$\frac{π}{3}$）的值；
（2）若y=f（x）在x∈R上有最小值-2，求a的值．

14．已知函数f（x）=ln（sinx+$\sqrt{si{n}^{2}x+α}$），-$\frac{π}{2}$≤x≤$\frac{π}{2}$，a为实常数，且f（x）为奇函数．
（1）求a的值；试说明函数f（x）的单调性，并求f（x）的值域；
（2）设g（x）为f（arcsinx）的反函数，并指出g（x）的定义域与值域．

4．${C}_{3}^{0}$+${C}_{4}^{1}$+${C}_{5}^{2}$+${C}_{6}^{3}$+…+${C}_{2013}^{2010}$的值为（　　）

${C}_{2013}^{3}$

${C}_{2014}^{3}$

${C}_{2014}^{4}$

${C}_{2013}^{4}$

11．设函数y=lnx与y=ax²-a的图象有公共点．且在公共点处有共同的切线．则a的值为（　　）

1或$\frac{1}{2}$

8．已知θ∈R，向量$\overrightarrow{a}$=（sinθ，cosθ），$\overrightarrow{b}$=（2，1），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则sin2θ（　　）

9．已知向量$\overrightarrow{a}$=（$\sqrt{3}$，-1），$\overrightarrow{b}$=（ $\sqrt{3}$，1），则＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{π}{3}$．