题目内容
4.${C}_{3}^{0}$+${C}_{4}^{1}$+${C}_{5}^{2}$+${C}_{6}^{3}$+…+${C}_{2013}^{2010}$的值为( )| A. | ${C}_{2013}^{3}$ | B. | ${C}_{2014}^{3}$ | C. | ${C}_{2014}^{4}$ | D. | ${C}_{2013}^{4}$ |
分析 直接运用组合数的两条性质,${C}_{n}^{m}$=${C}_{n}^{n-m}$和${C}_{n}^{m}$+${C}_{n}^{m+1}$=${C}_{n+1}^{m+1}$,运算求解.
解答 解:根据组合数的性质一:${C}_{n}^{m}$=${C}_{n}^{n-m}$,
所以,原式=${C}_{3}^{3}$+${C}_{4}^{3}$+${C}_{5}^{3}$+${C}_{6}^{3}$+…+${C}_{2013}^{3}$,
再根据组合数的性质二:${C}_{n}^{m}$+${C}_{n}^{m+1}$=${C}_{n+1}^{m+1}$,且${C}_{3}^{3}$=${C}_{4}^{4}$,
原式=${C}_{4}^{4}$+${C}_{4}^{3}$+${C}_{5}^{3}$+${C}_{6}^{3}$+…+${C}_{2013}^{3}$,
=${C}_{5}^{4}$+${C}_{5}^{3}$+${C}_{6}^{3}$+…+${C}_{2013}^{3}$,
=${C}_{6}^{4}$+${C}_{6}^{3}$+…+${C}_{2013}^{3}$,
=${C}_{2014}^{4}$,
故选:C.
点评 本题主要考查了组合及组合数公式的运算,尤其是组合的两点性质,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
9.若函数y=f(x)满足?x∈R,有f(1+x)=f(1-x)=f(x-1),则下列说法错误的是( )
| A. | f(x)的图象关于直线x=1对称 | B. | f(x)为奇函数 | ||
| C. | f(x)是周期为2的函数 | D. | f(x)为偶函数 |
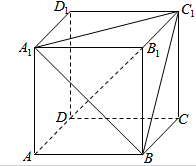 求证:正方体ABCD-A1B1C1D1中,对角线B1D与平面A1BC1互相垂直.
求证:正方体ABCD-A1B1C1D1中,对角线B1D与平面A1BC1互相垂直.