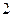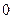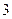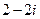题目内容
设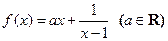 ,曲线y = f(x)在点(2,f(2))处的切线方程为y = x+3.
,曲线y = f(x)在点(2,f(2))处的切线方程为y = x+3.
(1)求f(x)的解析式;
(2)若x∈[2,3]时,f(x)≥bx恒成立,求实数b的取值范围.
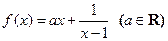 ,曲线y = f(x)在点(2,f(2))处的切线方程为y = x+3.
,曲线y = f(x)在点(2,f(2))处的切线方程为y = x+3.(1)求f(x)的解析式;
(2)若x∈[2,3]时,f(x)≥bx恒成立,求实数b的取值范围.
解:(1)由条件得f(2)=5,则(2,5)在
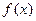 上,
上, 有
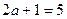 即
即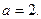
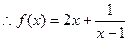
(2)x∈[2,3]时,f(x)≥bx恒成立等价于
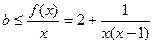 恒成立,
恒成立, 令
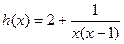 x∈[2,3],所以
x∈[2,3],所以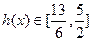
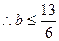
命题意图:
切线方程要注意“在点”和“过点”的区别;恒成立问题,存在性问题一般和最值、值域、单调性密切相关,当不等式两端都为变量时,一般要先分离变量.
切线方程要注意“在点”和“过点”的区别;恒成立问题,存在性问题一般和最值、值域、单调性密切相关,当不等式两端都为变量时,一般要先分离变量.

练习册系列答案
相关题目
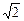 cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.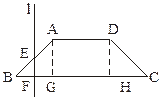
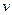 m/s和燃料的质量
m/s和燃料的质量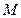 kg,火箭(除燃料外)的质量
kg,火箭(除燃料外)的质量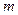 kg的函数关系是
kg的函数关系是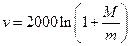 .当燃料质量是火箭质量的多少倍时,火箭的最大速度可达12km/s?
.当燃料质量是火箭质量的多少倍时,火箭的最大速度可达12km/s?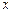 ,函数
,函数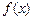 满足
满足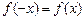 .若方程
.若方程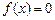 有2009个实数解,则这2009个实数解之和为
有2009个实数解,则这2009个实数解之和为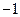 D 2
D 2 5)等于( )
5)等于( )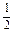 x(x+1)(39-2x),(x∈N*,且x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x.(x∈N*,且x≤12).(1)写出今年第x月的需求量f(x)件与x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2009年第几月份销售该商品的月利润最大,最大月利润为多少元?
x(x+1)(39-2x),(x∈N*,且x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x.(x∈N*,且x≤12).(1)写出今年第x月的需求量f(x)件与x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2009年第几月份销售该商品的月利润最大,最大月利润为多少元?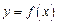 满足:①
满足:①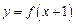 是偶函数;②在
是偶函数;②在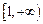 上为增函数。若
上为增函数。若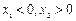 ,且
,且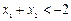 ,则
,则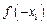 与
与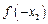 的大小关系是( )
的大小关系是( )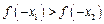

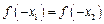
 上的函数
上的函数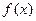 满足
满足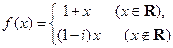 ,则
,则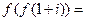 ( )
( )