题目内容
一个盒子里装有7张卡片, 其中有红色卡片4张, 编号分别为1, 2, 3, 4; 白色卡片3张, 编号分别为2, 3, 4．从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同)．
（1）求取出的4张卡片中, 含有编号为3的卡片的概率．
（2）再取出的4张卡片中, 红色卡片编号的最大值设为X, 求随机变量X的分布列和数学期望．
（1）求取出的4张卡片中, 含有编号为3的卡片的概率．
（2）再取出的4张卡片中, 红色卡片编号的最大值设为X, 求随机变量X的分布列和数学期望．
（1）
（2）
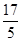
（2）
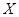 | 1 | 2 | 3 | 4 |
| P |  |  |  |  |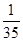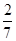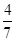
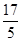
（1）设“取出的4张卡片中, 含有编号为3的卡片”为事件A，则
．
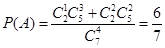所以取出的4张卡片中, 含有编号为3的卡片的概率为．
（2）随机变量X的所有可能取值为1，2，，3，4，
，
，
，
，
所以随机变量X的分布列是
随机变量X的数学期望
．
点评：本小题主要考查古典概型及其概率计算公式、互斥事件、离散型随机变量的分布列与数学期望等基础知识，考查运用概率知识解决简单实际问题的能力．
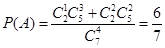．所以取出的4张卡片中, 含有编号为3的卡片的概率为
．（2）随机变量X的所有可能取值为1，2，，3，4，
，，，，所以随机变量X的分布列是
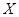| 1 | 2 | 3 | 4 |
| P | | | | |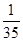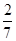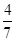
．点评：本小题主要考查古典概型及其概率计算公式、互斥事件、离散型随机变量的分布列与数学期望等基础知识，考查运用概率知识解决简单实际问题的能力．
练习册系列答案
相关题目
，否则其获胜的概率为
.
为比赛结束时甲的得分，求随机变量
.
，则D(ξ)＝________.
)=
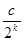,(k="1,2,3)," 其中c为常数，则E
.
.
，服用B有效的概率为
.