题目内容
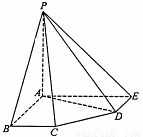
(本题14分)在五棱锥P-ABCDE中,PA=AB=AE=2,PB=PE=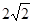 ,BC=DE=1,∠EAB=∠ABC=∠DEA=90°.
,BC=DE=1,∠EAB=∠ABC=∠DEA=90°.
(1)求证:PA⊥平面ABCDE;
(2)求二面角A-PD-E平面角的余弦值.
【答案】
(1)证明∵PA=AB=2a,PB=2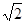 a,∴PA2+AB2=PB2,
a,∴PA2+AB2=PB2,
∴∠PAB=90°,即PA⊥AB.
同理PA⊥AE.3分∵AB∩AE=A,∴PA⊥平面ABCDE.
(2)∵∠AED=90°,∴AE⊥ED.
∵PA⊥平面ABCDE,∴PA⊥ED.
∴ED⊥平面PAE.过A作AG⊥PE于G,
∴DE⊥AG,∴AG⊥平面PDE.
过G作GH⊥PD于H,连AH,
由三垂线定理得AH⊥PD.
∴∠AHG为二面角A-PD-E的平面角.
在直角△PAE中,AG=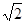 a.在直角△PAD中,AH=
a.在直角△PAD中,AH=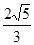 a,
a,
∴在直角△AHG中,sin∠AHG=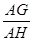 =
=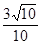 .
.
∴二面角A-PD-E平面角的余弦值为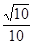
【解析】略

练习册系列答案
相关题目
 (本小题满分14分)在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD与底面ABCD垂直,PD=DC,E是PC的中点,作EF
(本小题满分14分)在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD与底面ABCD垂直,PD=DC,E是PC的中点,作EF 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 面PAD
面PAD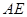 ;
;