题目内容
(本小题共14分)在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF PB交PB于点F
PB交PB于点F
⑴求证:PA//平面EDB
⑵求证:PB 平面EFD
平面EFD
⑶求二面角C-PB-D的大小

【答案】
解:建立空间直角坐标系,如图所示,点D为坐标原点,设DC=1…………1分
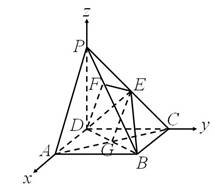
(1)证明:连接AC,AC交BD于点G,连接EG
依题意得A(1,0,0),P(0,0,1),E(0,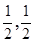 )
)
因为底面ABCD是正方形,所以点G是此正方形的中心,
故点G的坐标为(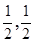 ,0),
,0),
且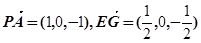 ,所以
,所以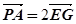
即PA//EG,而EG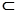 平面EDB,且PA
平面EDB,且PA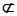 平面EDB,
平面EDB,
因此PA//平面EDB……6分
(2)证明:依题意得B(1,1,0),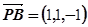 ,又
,又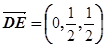
故 ,所以PB
,所以PB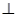 DE
DE
由已知EF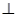 PB,且EF
PB,且EF DE=E,所以PB
DE=E,所以PB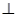 平面EFD……9分
平面EFD……9分
(3)解:已知PB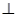 EF,由(2)可知PB
EF,由(2)可知PB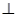 DF,
DF,
故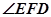 是二面角C—PB—D的平面角
是二面角C—PB—D的平面角
设点F的坐标为(x,y,z),则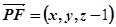
因为 所以(x,y,z-1)=k(1,1,-1)即x=k,y=k,z=1-k
所以(x,y,z-1)=k(1,1,-1)即x=k,y=k,z=1-k
为 ,所以(1,1,-1)
,所以(1,1,-1)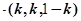 =k+k-1+k=3k-1=0
=k+k-1+k=3k-1=0
所以k=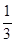 ,点F的坐标为(
,点F的坐标为(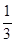 ,
,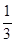 ,
,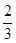 )
)
又点E的坐标为(0,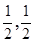 ),所以
),所以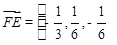
因为cos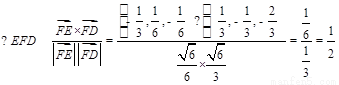
所以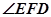 =60
=60 ,即二面角C—PB—D的大小为60
,即二面角C—PB—D的大小为60 ……14分
……14分
【解析】略

练习册系列答案
相关题目
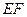 ⊥平面
⊥平面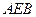 ,
, ,
,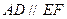 ,
,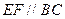 ,
,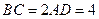 ,
, ,
,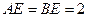 ,
,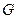 是
是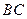 的
的 中点.
中点.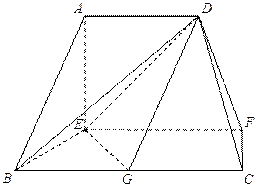
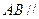 平面
平面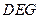 ;
;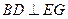 ;
;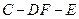 的余弦值.
的余弦值. 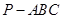 中,
中,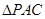 和
和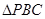 是边长为
是边长为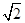 的等边三角形,
的等边三角形, ,
,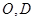 分别是
分别是 的中点.
的中点.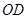 ∥平面
∥平面 ;
;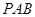 ⊥平面
⊥平面 ;
;
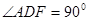 ,G是DF上一动点
,G是DF上一动点 GN垂直AC
GN垂直AC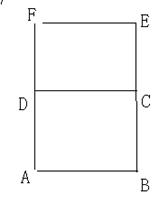

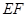 ⊥平面
⊥平面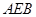 ,
, ,
,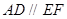 ,
,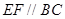 ,
,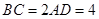 ,
,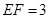 ,
,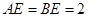 ,
,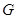 是
是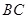 的中点.
的中点.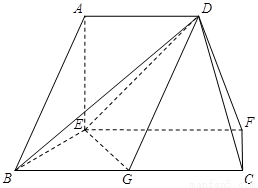
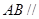 平面
平面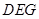 ;
;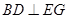 ;
;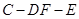 的余弦值.
的余弦值.