题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或33.
或33.
【解析】分析:(1)用代入法或加减法可消去参数![]() 得曲线
得曲线![]() 的直角坐标方程,由公式
的直角坐标方程,由公式 可化曲线
可化曲线![]() 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;
(2))将曲线![]() 的参数方程标准化为
的参数方程标准化为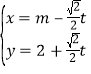 (
(![]() 为参数,
为参数,![]() )代入曲线
)代入曲线![]() 得
得![]() ,由
,由![]() 得
得![]() ,设
,设![]() 对应的参数为
对应的参数为![]() ,由题意得
,由题意得![]() ,分类代入可求得
,分类代入可求得![]() 值 .
值 .
详解:(1)![]() 的参数方程
的参数方程![]() ,消参得普通方程为
,消参得普通方程为![]()
![]() 的极坐标方程化为
的极坐标方程化为![]() 两边同乘
两边同乘![]() 得
得![]() 即
即![]() ;
;
(2)将曲线![]() 的参数方程标准化为
的参数方程标准化为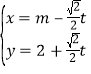 (
(![]() 为参数,
为参数,![]() )代入曲线
)代入曲线![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
设![]() 对应的参数为
对应的参数为![]() ,由题意得
,由题意得![]() 即
即![]() 或
或![]() ,
,
当![]() 时,
时,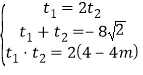 ,解得
,解得![]() ,
,
当![]() 时,
时, 解得
解得![]() ,
,
综上:![]() .
.

练习册系列答案
相关题目
【题目】某社区为了解居民参加体育锻炼的情况,从该社区随机抽取了18名男性居民和12名女性居民,对他们参加体育锻炼的情况进行问卷调查.现按是否参加体育锻炼将居民分成两类:甲类(不参加体育锻炼)、乙类(参加体育锻炼),结果如下表:
甲类 | 乙类 | |
男性居民 | 3 | 15 |
女性居民 | 6 | 6 |
(Ⅰ)根据上表中的统计数据,完成下面的![]() 列联表;
列联表;
男性居民 | 女性居民 | 总计 | |
不参加体育锻炼 | |||
参加体育锻炼 | |||
总计 |
(Ⅱ)通过计算判断是否有90%的把握认为参加体育锻炼与否与性别有关?
附: ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |


