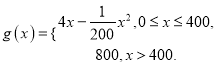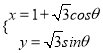题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)先求函数的定义域,求导通分后发现分母是含有参数的二次函数,根据其判别式进行分类讨论,由此求得函数的单调区间.(2)将![]() 和
和![]() 代入原函数,可将原不等式化简为
代入原函数,可将原不等式化简为![]() 恒成立,利用分离常数法,可将问题转化为切线的斜率来求解.
恒成立,利用分离常数法,可将问题转化为切线的斜率来求解.
试题解析:(1)![]() ,
,
令![]() ,判别式为:
,判别式为:![]() ,
,
①:当![]() ,得
,得![]() ,
,
此时![]() ,从而
,从而![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
②:当![]() ,即
,即![]() ,
,
令![]() ,得方程的根
,得方程的根
![]() (舍去),
(舍去),![]() ,
,
若![]() ,此时
,此时![]() ,
,![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减,
单调递减,
若![]() ,此时
,此时![]() 的对称轴为
的对称轴为![]() ,
,
![]() ,
,
∴![]() ,从而
,从而![]() 在
在![]() 上单调递增.
上单调递增.
综上:当![]() ,
,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() 单调递减.
单调递减.
(2)由题意有![]() 恒成立,
恒成立,
即![]() ,
,
即![]() 恒成立,
恒成立,
当![]() 时,不等式显然恒成立,
时,不等式显然恒成立,
当![]() 时,
时,![]() ,
,
所以![]() ,则
,则![]() ,于是
,于是
![]() ,在
,在![]() 上恒成立,
上恒成立,
令![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,且
,且![]() 两点在
两点在![]() 的图象上,
的图象上,
又![]() ,
,
故![]() ,
,
所以![]() ,
,
故![]() 为所求.
为所求.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】随着移动互联网时代的到来,手机的使用非常普遍,“低头族”随处可见。某校为了解家长和教师对学生带手机进校园的态度,随机调查了100位家长和教师,得到情况如下表:
教师 | 家长 | |
反对 | 40 | 20 |
支持 | 20 | 20 |
(1)是否有95%以上的把握认为“带手机进校园与身份有关”,并说明理由;
(2)把以上频率当概率,随机抽取3位教师,记其中反对学生带手机进校园的人数为X,求随机变量X的分布列和数学期望.
附: 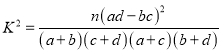
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
【题目】某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J) | 1.6×1019 | 3.2×1019 | 4.5×1019 | 6.4×1019 |
震级(里氏) | 5.0 | 5.2 | 5.3 | 5.4 |
注:地震强度是指地震时释放的能量.
地震强度(x)和震级(y)的模拟函数关系可以选用y=alg x+b(其中a,b为常数).利用散点图(如图)可知a的值等于________.(取lg 2=0.3进行计算)