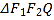题目内容
【题目】已知函数![]() 有且仅有三个零点,并且这三个零点构成等差数列,则实数a的值为_______.
有且仅有三个零点,并且这三个零点构成等差数列,则实数a的值为_______.
【答案】![]() 或
或![]()
【解析】
利用函数与方程之间的关系,转化为两个函数交点问题,结合分段函数的性质进行转化求解即可.
函数![]() 0,
0,
得|x+a|![]() a=3,
a=3,
设g(x)=|x+a|![]() a,h(x)=3,
a,h(x)=3,
则函数g(x)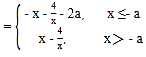 ,
,
不妨设f(x)=0的3个根为x1,x2,x3,且x1<x2<x3,
当x>﹣a时,由f(x)=0,得g(x)=3,即x![]() 3,
3,
得x2﹣3x﹣4=0,得(x+1)(x﹣4)=0,
解得x=﹣1,或x=4;
若 ①﹣a≤﹣1,即a≥1,此时 x2=﹣1,x3=4,由等差数列的性质可得x1=﹣6,
由f(﹣6)=0,即g(﹣6)=3得6![]() 2a=3,解得a
2a=3,解得a![]() ,满足f(x)=0在(﹣∞,﹣a]上有一解.
,满足f(x)=0在(﹣∞,﹣a]上有一解.
若②﹣1<﹣a≤4,即﹣4≤a<1,则f(x)=0在(﹣∞,﹣a]上有两个不同的解,不妨设x1,x2,其中x3=4,
所以有x1,x2是﹣x![]() 2a=3的两个解,即x1,x2是x2+(2a+3)x+4=0的两个解.
2a=3的两个解,即x1,x2是x2+(2a+3)x+4=0的两个解.
得到x1+x2=﹣(2a+3),x1x2=4,
又由设f(x)=0的3个根为x1,x2,x3成差数列,且x1<x2<x3,得到2x2=x1+4,
解得:a=﹣1![]() (舍去)或a=﹣1
(舍去)或a=﹣1![]() .
.
③﹣a>4,即a<﹣4时,f(x)=0最多只有两个解,不满足题意;
综上所述,a![]() 或﹣1
或﹣1![]() .
.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案【题目】某人事部门对参加某次专业技术考试的100人的成绩进行了统计,绘制的频率分布直方图如图所示.规定80分以上者晋级成功,否则晋级失败(满分为100分).
(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关.
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |

参考公式:![]() ,其中
,其中![]()
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为![]() 的雾霾天数.
的雾霾天数.