题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 都相切,切点分别为
都相切,切点分别为![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)分类讨论,详见解析;(2)详见解析.
【解析】
(1)首先写出函数![]() 定义域为
定义域为![]() ,求得
,求得![]() ,对
,对![]() 的范围进行讨论,从而确定出
的范围进行讨论,从而确定出![]() 的符号,确定出函数
的符号,确定出函数![]() 的单调性;
的单调性;
(2)可以从两个角度去分析,方法一是根据导数的几何意义,写出直线![]() 的方程为
的方程为![]() ,即
,即![]() ,也可以写成
,也可以写成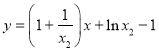 ,根据两条直线是同一条直线,得到
,根据两条直线是同一条直线,得到![]() ,且
,且![]() ,对式子进行整理可以得到
,对式子进行整理可以得到![]() ,构造函数
,构造函数![]() ,利用导数研究该函数的单调性及最值,从而可以证得结果;方法二是根据两条切线的斜率想的得到
,利用导数研究该函数的单调性及最值,从而可以证得结果;方法二是根据两条切线的斜率想的得到 ,进一步可以得到
,进一步可以得到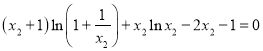 ,构造函数
,构造函数![]() ,利用导数研究该函数的单调性及最值得到结果.
,利用导数研究该函数的单调性及最值得到结果.
(1)![]() 定义域为
定义域为![]() ,
,
因为![]() ,
,
若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
若![]() ,则当
,则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)证法一:
证明:对于曲线![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
即![]() ,即
,即![]() ①.
①.
对于曲线![]() ,因为
,因为![]() ,所以
,所以![]()
所以![]() ,
,
直线![]() 的方程为
的方程为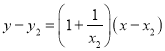 ,
,
即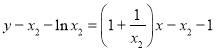 ,即
,即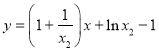 ②.
②.
因为①与②表示同一条直线,所以![]() ③,
③,
且![]() ④,
④,
④÷③,得![]() ,
,
所以![]() .
.
令![]() ,
,
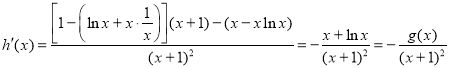 ,
,
由(1)知,![]() 在
在![]() 单调递增又
单调递增又![]()
![]() ∴
∴![]()
![]() 有唯一零点
有唯一零点![]() ,
,
且当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
所以![]() ,
,
又![]() ,即
,即![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
证法二:
证明:因为![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以直线![]() 的斜率为
的斜率为![]() ,
,
所以![]() ,所以
,所以 ,
,
又因为 ,
,
所以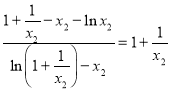 ,
,
所以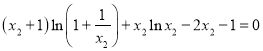 ,
,
令![]() ,
,
所以![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
又因为![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]() ,
,
且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
因为![]() ,所以
,所以![]() 在
在![]() 递减,
递减,
所以当![]() 时,
时, ,
,
所以![]() 在
在![]() 内无零点,
内无零点,
因为![]() 是
是![]() 的零点且
的零点且![]() ,所以
,所以![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数 | 未损坏餐椅数 | 总计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总计 | 80 | 320 | 400 |
![]() 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
![]() 请说明是否有
请说明是否有![]() 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神
有关?![]() 参考公式:
参考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|