题目内容
【题目】已知函数![]() (其中
(其中![]() 是自然对数的底数.)
是自然对数的底数.)
(1)讨论函数![]() 的单调性;
的单调性;
(2)当函数![]() 有两个零点
有两个零点![]() ,
, ![]() 时,证明:
时,证明: ![]() .
.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)由已知中函数的解析式,求出导函数的解析式,对![]() 进行分类讨论,确定
进行分类讨论,确定![]() 在不同情况下导函数的符号,进而可得函数的单调性.
在不同情况下导函数的符号,进而可得函数的单调性.
(2)先求出![]() ,令
,令![]() ,求出
,求出![]() ,问题转化为证明
,问题转化为证明![]() ,构造函数
,构造函数![]() ,通过函数的单调性证明即可.
,通过函数的单调性证明即可.
试题解析:(1)解:因为![]() ,
,
当![]() 时,令
时,令![]() 得
得![]() ,所以当
,所以当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 恒成立,故此时函数
恒成立,故此时函数![]() 在
在![]() 上单调递增.
上单调递增.
(2)证明:当![]() 时,由(1)知函数
时,由(1)知函数![]() 单调递增,不存在两个零点,所以
单调递增,不存在两个零点,所以![]() ,
,
设函数![]() 的两个零点为
的两个零点为![]() ,
, ![]() ,且
,且![]() . 由题意得:
. 由题意得:  ,
, ![]() ②-①得:
②-①得: ![]()
令![]() ,则
,则![]() ∴③可化为:
∴③可化为: ![]()
![]()
要证: ![]() 只需证:
只需证: ![]()
即证: ![]()
构造函数![]() ,则
,则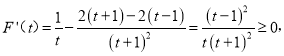
![]() 在
在![]() 单调递增,
单调递增,![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某公司经营一种二手机械,对该型号机械的使用年数![]() 与再销售价格
与再销售价格![]() (单位:百万元/台)进行统计整理,得到如下关系:
(单位:百万元/台)进行统计整理,得到如下关系:
使用年数 | 2 | 4 | 6 | 8 | 10 |
再销售价格 | 16 | 13 | 9.5 | 7 | 5 |
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)该机械每台的收购价格为![]() (百万元),根据(1)中所求的回归方程,预测
(百万元),根据(1)中所求的回归方程,预测![]() 为何值时,此公司销售一台该型号二手机械所获得的利润
为何值时,此公司销售一台该型号二手机械所获得的利润![]() 最大?
最大?
附:参考公式: ,
,![]() .
.