题目内容
在平面直角坐标系xoy中,直线l与抛物线![]() 相交于不同的A、B两点.
相交于不同的A、B两点.
(Ⅰ)如果直线l过抛物线的焦点,求![]() 的值;
的值;
(Ⅱ)如果![]() 证明直线l必过一定点,并求出该定点
证明直线l必过一定点,并求出该定点
(Ⅰ)![]() 的值=-3;(Ⅱ)直线l过定点(2,0)。
的值=-3;(Ⅱ)直线l过定点(2,0)。
解析:
(Ⅰ)由题意:抛物线焦点为(1,0)
设![]() 消去x得
消去x得
![]()
则![]()
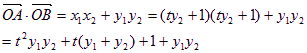
=![]()
(Ⅱ)设![]() 消去x,得
消去x,得
![]()
则y1+y2=4t y1y2=-4b
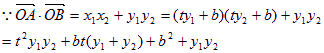
=![]()
令![]()
∴直线l过定点(2,0)

练习册系列答案
相关题目
题目内容
在平面直角坐标系xoy中,直线l与抛物线![]() 相交于不同的A、B两点.
相交于不同的A、B两点.
(Ⅰ)如果直线l过抛物线的焦点,求![]() 的值;
的值;
(Ⅱ)如果![]() 证明直线l必过一定点,并求出该定点
证明直线l必过一定点,并求出该定点
(Ⅰ)![]() 的值=-3;(Ⅱ)直线l过定点(2,0)。
的值=-3;(Ⅱ)直线l过定点(2,0)。
(Ⅰ)由题意:抛物线焦点为(1,0)
设![]() 消去x得
消去x得
![]()
则![]()
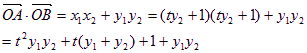
=![]()
(Ⅱ)设![]() 消去x,得
消去x,得
![]()
则y1+y2=4t y1y2=-4b
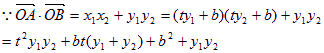
=![]()
令![]()
∴直线l过定点(2,0)
