题目内容
【题目】已知不等式![]() .
.
(1)是否存在实数m,使不等式对任意![]() 恒成立?并说明理由.
恒成立?并说明理由.
(2)若不等式对任意![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(3)若对于![]() ,不等式恒成立,求实数x的取值范围.
,不等式恒成立,求实数x的取值范围.
【答案】(1)不存在;(2)![]() ;(3)
;(3)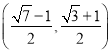 .
.
【解析】
(1)对![]() 分成
分成![]() 两种情况,结合一元一次不等式的解法、一元二次不等式恒成立问题求解策略,由此求得
两种情况,结合一元一次不等式的解法、一元二次不等式恒成立问题求解策略,由此求得![]() 的取值范围.(2)构造函数
的取值范围.(2)构造函数![]() ,对
,对![]() 分成
分成![]() 三种情况,利用二次函数的性质列不等式,通过解不等式求得
三种情况,利用二次函数的性质列不等式,通过解不等式求得![]() 的取值范围.(3)构造函数
的取值范围.(3)构造函数![]() ,交换主参变量,根据
,交换主参变量,根据![]() 两种情况,结合一元一次函数的性质,求得实数
两种情况,结合一元一次函数的性质,求得实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() ,不可能恒成立;当
,不可能恒成立;当![]() 时,
时,![]() ,即
,即![]() ,不存在.
,不存在.
因此,不存在实数![]() ,使不等式对任意
,使不等式对任意![]() 恒成立.
恒成立.
(2)令![]() .
.
当![]() 时,
时,![]() 解得
解得![]() ,符合题意.
,符合题意.
当![]() 时,
时,![]() ,不成立;
,不成立;
当![]() 时,∵抛物线对称轴
时,∵抛物线对称轴![]() ,抛物线开口向下,∴只需
,抛物线开口向下,∴只需![]() ,与
,与![]() 矛盾.
矛盾.
综上所述,![]() .
.
(3)设![]() .
.
①当![]() ,即
,即![]() 时,要使当
时,要使当![]() 时,
时,![]() 恒成立,有
恒成立,有
![]() 即
即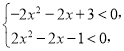 得
得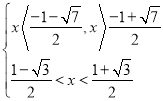
∴![]() ;
;
②当![]() ,即
,即![]() 时,经检验
时,经检验![]() 满足题意.
满足题意.
由①②可知,所求的![]() 的取值范围是
的取值范围是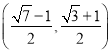 .
.

练习册系列答案
相关题目