题目内容
【题目】已知椭圆C:![]() 1(a>b>0),A(﹣a,0),B(0,﹣b),P为C上位于第一象限的动点,PA交y轴于点E,PB交x轴于点F.
1(a>b>0),A(﹣a,0),B(0,﹣b),P为C上位于第一象限的动点,PA交y轴于点E,PB交x轴于点F.
(1)探究四边形AEFB的面积是否为定值,说明理由;
(2)当△PEF的面积达到最大值时,求点P的坐标.
【答案】(1)面积为定值,详见解析(2)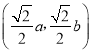
【解析】
(1)设![]() ,写出直线方程求出
,写出直线方程求出![]() 坐标,计算面积
坐标,计算面积![]() 可得定值;
可得定值;
(2)求出![]() 到直线
到直线![]() 的距离
的距离![]() ,由(1)知
,由(1)知![]() 面积最大时,
面积最大时,![]() 面积最大,从而只要
面积最大,从而只要![]() 最大即可,
最大即可,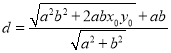 ,由
,由![]() 在椭圆上,利用基本不等式可得
在椭圆上,利用基本不等式可得![]() 的最大值,从而得出结论.
的最大值,从而得出结论.
(1)设P(x0,y0),四边形AEFB的面积为定值,证明如下:
则PA的方程为![]() ,可得
,可得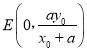 ,故
,故![]() ,
,
同理可得,![]() ,
,
从而四边形AEFB的面积为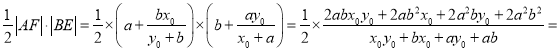 ab,
ab,
所以四边形AEFB的面积为ab.
(2)由题设知直线AB:bx+ay+ab=0,
点P到AB的距离为d,则![]() ,
,
由(1)可知,当且仅当△ABP的面积最大时,△PEF的面积最大,所以当d取最大值时,△PEF的面积最大,
由于P在C上,故![]() ,可得
,可得![]() ,
,
所以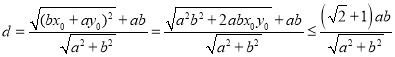 ,
,
当且仅当![]() ,即
,即![]() ,
,![]() 时等号成立,
时等号成立,
所以点P的坐标为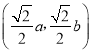 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目