题目内容
2.在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2cosA-1)sinB+2cosA=1.(1)求A的大小;
(2)若5b2=a2+2c2,求$\frac{sinB}{sinC}$的值.
分析 (1)化简已知的式子,结合角的范围求出cosA的值,由特殊角的余弦值求出角A;
(2)由(1)和余弦定理列出方程,把条件代入化简后转化为关于$\frac{b}{c}$的二次方程,求出$\frac{b}{c}$的值,根据正弦定理即可求出$\frac{sinB}{sinC}$的值.
解答 解:(1)∵(2cosA-1)sinB+2cosA=1,
∴(2cosA-1)(sinB+1)=0,
∵0<B<π,∴sinB>0,则$cosA=\frac{1}{2}$,
∵0<A<π,∴$A=\frac{π}{3}$;
(2)在△ABC中,由余弦定理得:a2=b2+c2-2bccosA=b2+c2-bc,
∵5b2=a2+2c2,∴5b2=b2+c2-bc+2c2,
化简得4b2+bc-3c2=0,
∴$4{(\frac{b}{c})^2}+\frac{b}{c}-3=0$,∴$(\frac{b}{c}+1)(4•\frac{b}{c}-3)=0$,
解得$\frac{b}{c}=-1(舍),或\frac{b}{c}=\frac{3}{4}$,
由正弦定理得,$\frac{sinB}{sinC}=\frac{b}{c}=\frac{3}{4}$.
点评 本题考查正弦、余弦定理的综合应用,以及化简、变形能力,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
13.下列四组函数中,表示相等函数的是( )
| A. | f(x)=$\sqrt{x}$,g(x)=($\sqrt{x}$)2 | |||||||||
| B. | f(x)=2lgx,g(x)=lgx2 | |||||||||
| C. | f(x)=$\sqrt{x-1}$$\sqrt{x+1}$,g(x)=$\sqrt{{x}^{2}-1}$ | |||||||||
| D. | f(x)=$\left\{\begin{array}{l}{1,x≤1}\\{2,1<x<2}\\{3,x≥2}\end{array}\right.$,
|
7.已知命题p:关于x的函数y=x2-3ax+4在[1,+∞)上是增函数,命题q:函数y=(2a-1)x为减函数,若“p且q”为真命题,则实数a的取值范围是( )
| A. | (-∞,$\frac{2}{3}$] | B. | (0,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,$\frac{2}{3}$] | D. | ($\frac{1}{2}$,1) |
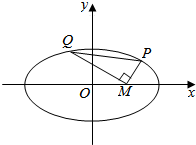 设椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A、B,点P在椭圆上,且异于A、B两点,O为坐标原点
设椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A、B,点P在椭圆上,且异于A、B两点,O为坐标原点