Question

【题目】为了了解湖南各景点在大众中的熟知度，随机对15～65岁的人群抽样了n人，回答问题“湖南省有哪几个著名的旅游景点？”统计结果如下图表．

组号	分组	回答正确的人数	回答正确的人数 占本组的频率
第1组	[15，25）	a	0.5
第2组	[25，35）	18	x
第3组	[35，45）	b	0.9
第4组	[45，55）	9	0.36
第5组	[55，65]	3	y

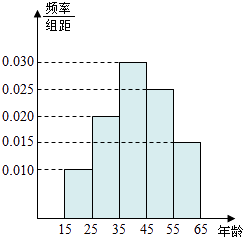
（1）分别求出a，b，x，y的值；
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，求第2，3，4组每组各抽取多少人？
（3）在（2）抽取的6人中随机抽取2人，求所抽取的人中恰好没有第3组人的概率．

Answer 1

【答案】
（1）解：由频率表中第4组数据可知，第4组总人数为 ，

再结合频率分布直方图可知n= ，

∴a=100×0.01×10×0.5=5，b=100×0.03×10×0.9=27，

；

（2）解：因为第2，3，4组回答正确的人数共有54人，

∴利用分层抽样在54人中抽取6人，每组分别抽取的人数为：第2组： 人；第3组： 人；第4组： 人

（3）解：设第2组2人为：A1，A2；第3组3人为：B1，B2，B3；第4组1人为：C1．

则从6人中随机抽取2人的所有可能的结果为：（A1，A2），（A1，B1），（A1，B2），（A1，B3），（A1，C1），

（A2，B1），（A2，B2），（A2，B3），（A2，C1），（B1，B2），（B1，B3），（B1，C1），（B2，B3），（B2，C1），（B3，C1）共15个基本事件，

其中恰好没有第3组人共3个基本事件，

∴所抽取的人中恰好没有第3组人的概率是：

【解析】（1）由频率表中第4组数据可知，第4组的频数为25，再结合频率分布直方图求得n，a，b，x，y的值；（2）因为第2，3，4组回答正确的人数共有54人，抽取比例为 ，根据抽取比例计算第2，3，4组每组应抽取的人数；（3）列出从6人中随机抽取2人的所有可能的结果，共15基本事件，其中恰好没有第3组人共3个基本事件，利用古典概型概率公式计算．
【考点精析】本题主要考查了频率分布直方图的相关知识点，需要掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息才能正确解答此题．