题目内容
【题目】已知函数f(x)=2x
(1)试求函数F(x)=f(x)+f(2x),x∈(﹣∞,0]的最大值;
(2)若存在x∈(﹣∞,0),使|af(x)﹣f(2x)|>1成立,试求a的取值范围;
(3)当a>0,且x∈[0,15]时,不等式f(x+1)≤f[(2x+a)2]恒成立,求a的取值范围.
【答案】(1)2 ; (2)a<0,或a>2; .(3)a≥1.
【解析】
(1)把f(x)代入到F(x)中化简得到F(x)的解析式求出F(x)的最大值即可;
(2)可设2x=t,存在t∈(0,1)使得|t2﹣at|>1,讨论求出解集,让a大于其最小,小于其最大即可得到a的取值范围;
(3)不等式f(x+1)≤f[(2x+a)2]恒成立即为![]() 恒成立即要
恒成立即要![]() ,根据二次函数求最值的方法求出最值即可列出关于a的不等式,求出解集即可.
,根据二次函数求最值的方法求出最值即可列出关于a的不等式,求出解集即可.
(1)∵x∈(﹣∞,0],F(x)=f(x)+f(2x)=2x+4x,令2x=t,(0<t≤1),
即有F(x)=t2+t=![]() 在
在![]() 单调递增,
单调递增,![]() 时
时![]()
(2)令2x=t,则存在t∈(0,1)使得|t2﹣at|>1
所以存在t∈(0,1)使得t2﹣at>1,或t2﹣at<﹣1.
即存在t∈(0,1)使得![]() ,∴a<0,或a>2;
,∴a<0,或a>2;
(3)由f(x+1)≤f[(2x+a)2]得x+1≤(2x+a)2恒成立
因为a>0,且x∈[0,15],所以问题即为![]() 恒成立,∴
恒成立,∴![]() .
.
设m(x)=![]() 令
令![]() ,∴
,∴![]() .
.
所以,当t=1时,m(x)max=1,∴a≥1.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】为了了解湖南各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |
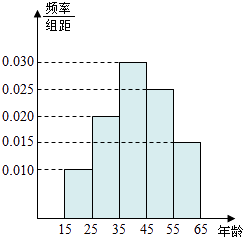
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
