题目内容

20．解关于x的不等式（x-2）（ax-2）＞0．

分析 对参数a的取值范围进行讨论，分类解不等式．

解答 解：当a=0时，解得x＜2，故不等式的解集为（-∞，2），
当a＜0时，不等式（x-2）（ax-2）＞0转化为为（x-2）（x-$\frac{2}{a}$）＜0，解得$\frac{2}{a}$＜x＜2，故不等式的解集为（$\frac{2}{a}$，2），
当a＞0时，不等式（x-2）（ax-2）＞0转化为为（x-2）（x-$\frac{2}{a}$）＞0，
①当0＜a＜1时，解得x＜2，或x＞$\frac{2}{a}$，故不等式的解集为（-∞，2）∪（$\frac{2}{a}$，+∞），
②当a＞1时，解得x＜$\frac{2}{a}$，或x＞2，故不等式的解集为（-∞，$\frac{2}{a}$）∪（2，+∞），
③当a=1时，即（x-2）2＞0，解得x≠2，故不等式的解集为（-∞，2）∪（2，+∞）．

点评 本题考查一元二次不等式的解法，解题的关键是对参数的范围进行分类讨论，分类解不等式，此题是一元二次不等式解法中的难题，易因为分类不清与分类有遗漏导致解题失败，解答此类题时要严谨，避免考虑不完善出错．

练习册系列答案
相关题目
10．已知$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（1，1），则$\overrightarrow{b}$-3$\overrightarrow{a}$与$\overrightarrow{a}$的夹角的余弦值为$-\frac{2\sqrt{5}}{5}$．
11．已知g（x）=ax+1，f（x）=$\left\{\begin{array}{l}{2{\;}^{x}-1，0≤x≤2}\\{-x{\;}^{2}，-2≤x＜0}\end{array}\right.$，对?x1∈[-2，2]，?x2∈[-2，2]，使g（x1）=f（x2）成立，求实数a的取值范围．
8．已知a＞0，b＞0，比较aabb和（ab）${\;}^{\frac{a+b}{2}}$的大小关系．
15．从7名男生5名女生中选出5人，分别求符合下列条件的选法种数有多少种：
（1）A、B不全当选；
（2）至少有2名女生当选；
（3）选出5名同学，让他们分别担任体育委员、文娱委员等5个班委，但体育委员由男生担任，文娱委员由女生担任．
5．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=3，它们的夹角为120°，那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{13}$．
12．如果执行如图的程序框图，输出的结果为（　　）
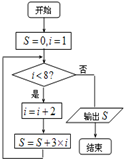
A．43B．69C．72D．54
9．已知$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{{e}_{3}}$均为单位向量，其中任何两个向量的夹角均为120°，则|$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$+$\overrightarrow{{e}_{3}}$|=（　　）
A．3B．$\sqrt{3}$C．$\sqrt{2}$D．0
10．以抛物线y=$\frac{1}{4}$x2的焦点为圆心，且过坐标原点的圆的方程为（　　）
A．x2+y2-x=0B．x2+y2-2x=0C．x2+y2-y=0D．x2+y2-2y=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网