题目内容
设双曲线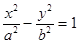
的虚轴长为２，焦距为
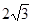，则双曲线的渐近线方程为( )
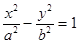
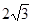的虚轴长为２，焦距为，则双曲线的渐近线方程为( )A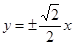． | B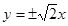． | C． | D． |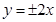
A
试题分析：由双曲线的方程
与题意，可知
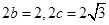，即
，∴
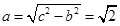，所以双曲线的渐近线方程为
，故选A.
练习册系列答案
阅读快车系列答案
相关题目
试题分析：由双曲线的方程
与题意，可知，即，∴，所以双曲线的渐近线方程为，故选A.阅读快车系列答案题目内容
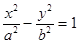
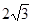的虚轴长为２，焦距为，则双曲线的渐近线方程为( )| A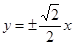． | B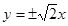． | C． | D． |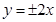
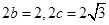与题意，可知，即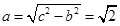，∴，所以双曲线的渐近线方程为，故选A.阅读快车系列答案
和
，且|
）在该椭圆上．
与椭圆C相交于A，B两点，若
A
，求以
的离心率是
，
分别是椭圆
的左、右两个顶点，点
是椭圆
是
轴上位于
右侧的一点，且满足
．
，再作直线
与椭圆
，直线
交直线
．求证：以线段
为直径的圆恒过定点，并求出定点的坐标．
，|BC|＝2．E，F，G，H分别是矩形四条边的中点，分别以HF，EG所在的直线为x轴，y轴建立平面直角坐标系，已知
＝λ
，
＝λ
，其中0＜λ＜1．
＋y2＝1上；
：
（
）过点
，且椭圆
.
在直线
上，过
两点，且
中点，再过
.证明：直线
恒过定点，并求出该定点的坐标.
＝1(a>b>0)上两点，已知m＝
，n＝
，若m·n＝0且椭圆的离心率e＝
，短轴长为2，O为坐标原点．
，则方程
表示的曲线不可能是（ ）
交双曲线
于
两点，
为双曲线
上异于
的斜率之积为( )
，
分别为双曲线
，
的左、右焦点，若在右支上存在点
，使得点
到直线
的距离为
，则该双曲线的离心率的取值范围是( )
