题目内容
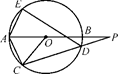
如图,在△ABC中,∠C=90°,BE是角平分线,DE⊥BE交AB于D,圆O是△BDE的外接圆.
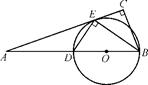
(1)求证:AC是圆O的切线;
(2)如果AD=6,AE=6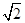 ,求BC的长.
,求BC的长.

(1)求证:AC是圆O的切线;
(2)如果AD=6,AE=6
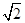 ,求BC的长.
,求BC的长.(1)见解析(2)4
(1)证明:连OE,∵BE⊥DE,
∴O点为BD的中点.
∵OB=OE,∴∠OEB=∠OBE.
∵∠OEC=∠OEB+∠CEB=∠OBE+∠CEB=∠CEB+∠CBE=90°,即OE⊥AC.
又E是AC与圆O的公共点,∴AC是圆O的切线.
(2)解:∵AE是圆的切线,∴∠AED=∠ABE.
又∠A共用,∴△ADE∽△AEB,
∴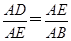 ,即
,即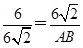 ,解得AB=12,
,解得AB=12,
∴圆O的半径为3.
又∵OE∥BC,∴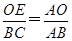 ,即
,即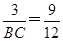 ,解得BC=4.
,解得BC=4.
∴O点为BD的中点.
∵OB=OE,∴∠OEB=∠OBE.
∵∠OEC=∠OEB+∠CEB=∠OBE+∠CEB=∠CEB+∠CBE=90°,即OE⊥AC.
又E是AC与圆O的公共点,∴AC是圆O的切线.
(2)解:∵AE是圆的切线,∴∠AED=∠ABE.
又∠A共用,∴△ADE∽△AEB,
∴
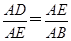 ,即
,即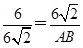 ,解得AB=12,
,解得AB=12,∴圆O的半径为3.
又∵OE∥BC,∴
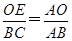 ,即
,即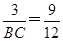 ,解得BC=4.
,解得BC=4.
练习册系列答案
相关题目

 ·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设
·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设 =k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
=k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.

 , PD =" 2DA" =" 2," 则PE = .
, PD =" 2DA" =" 2," 则PE = . 