题目内容
(2013•广东模拟)数列{an}的各项均为正数,sn为其前n项和,对于任意n∈N*,总有an,sn,an2成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)正数数列{cn}中,an+1=(cn)n+1,(n∈N°).求数列{cn}中的最大项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)正数数列{cn}中,an+1=(cn)n+1,(n∈N°).求数列{cn}中的最大项.
分析:(Ⅰ)由已知可得2sn=an+an2,则2sn-1=an+an-12(n≥2),两式相减整理可得an-an-1=1,令n=1解得a1,结合等差数列的通项公式可求
(Ⅱ)由已知,an+1=(cn)n+1,分别令n=1,2,3,4可求c1,c2,c3,c4,结合几项的值,猜想{cn}的单调性,然后构造函数f(x)=
,结合导数判断该函数在[3,+∞)内的单调性,进而可知{cn}的单调性,即可判断
(Ⅱ)由已知,an+1=(cn)n+1,分别令n=1,2,3,4可求c1,c2,c3,c4,结合几项的值,猜想{cn}的单调性,然后构造函数f(x)=
| lnx |
| x |
解答:(Ⅰ)解:由已知:对于任意n∈N*,总有2sn=an+an2①成立
∴2sn-1=an+an-12(n≥2)②
①--②得2an=an+an2-an-1-an-12
∴an+an-1=(an+an-1)(an-an-1)
∵各项都均为正数,
∴an-an-1=1 (n≥2)
∴数列{an}是公差为1的等差数列
又n=1时,2s1=a1+a12,解得a1=1
∴an=n.
(Ⅱ)由已知 a2=c12=2可得c1=
a3=c23=3可得,c2=
a4=c34=4可得c3=
a5=c45=5可得c4=
易得 c1<c2>c3>c4
猜想 n≥2 时,{cn}是递减数列.
令f(x)=
∴f′(x)=
=
∵当x≥3时lnx>1,则1-lnx<0,即f‘(x)<0
∴在[3,+∞)内f(x)为单调递减函数.
由an+1=(cn)n+1,可得cn=
.
∴n≥2 时,{lncn}是递减数列.即{cn}是递减数列.
又c1<c2,
∴数列{cn}中的最大项为c2=
.
∴2sn-1=an+an-12(n≥2)②
①--②得2an=an+an2-an-1-an-12
∴an+an-1=(an+an-1)(an-an-1)
∵各项都均为正数,
∴an-an-1=1 (n≥2)
∴数列{an}是公差为1的等差数列
又n=1时,2s1=a1+a12,解得a1=1
∴an=n.
(Ⅱ)由已知 a2=c12=2可得c1=
| 2 |
a3=c23=3可得,c2=
| 3 | 3 |
a4=c34=4可得c3=
| 4 | 4 |
a5=c45=5可得c4=
| 5 | 5 |
易得 c1<c2>c3>c4
猜想 n≥2 时,{cn}是递减数列.
令f(x)=
| lnx |
| x |
∴f′(x)=
| ||
| x2 |
| 1-lnx |
| x2 |
∵当x≥3时lnx>1,则1-lnx<0,即f‘(x)<0
∴在[3,+∞)内f(x)为单调递减函数.
由an+1=(cn)n+1,可得cn=
| ln(n+1) |
| n+1 |
∴n≥2 时,{lncn}是递减数列.即{cn}是递减数列.
又c1<c2,
∴数列{cn}中的最大项为c2=
| 3 | 3 |
点评:本题主要考查了利用数列的递推公式求解数列的通项公式,等差数列的通项公式的应用及利用函数的单调性判断相应数列的单调性及利用单调性判断数列取得的最大项

练习册系列答案
相关题目
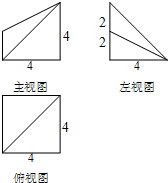 (2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为
(2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为