题目内容
【题目】已知数列{an}的首项a1=2,且an=2an﹣1﹣1(n∈N* , N≥2)
(1)求证:数列{an﹣1}为等比数列;并求数列{an}的通项公式;
(2)求数列{nan﹣n}的前n项和Sn .
【答案】
(1)证明:由an=2an﹣1﹣1,得an﹣1=2(an﹣1﹣1),
∴数列{an﹣1}构成首项为a1﹣1=1,公比q=2的等比数列,
∴an﹣1=2n﹣1,即an=2n﹣1+1
(2)解:∵nan﹣n=n2n﹣1+n﹣n=n2n﹣1,
∴Sn=120+221+322+…+n2n﹣1,①,
2Sn=121+222+323+…+n2n,②,
②﹣①,得:Sn=﹣20﹣21﹣22﹣…﹣2n﹣1+n2n=﹣ ![]() +n2n=n2n+1﹣2n=(n﹣1)2n+1.
+n2n=n2n+1﹣2n=(n﹣1)2n+1.
【解析】(1)已知通项公式变形,利用等比数列的性质判断得证,求出数列{an}的通项公式即可;(2)根据题意表示出数列{nan﹣n}的前n项和Sn , 利用数列的递推式确定出Sn通项公式即可.
【考点精析】本题主要考查了等比数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系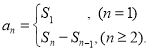 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目