题目内容
15.已知函数f(x)=|x-2|,若b≠0,且a,b∈R时,都有不等式|a+b|+|a-2b|≥|b|•f(x)成立,则实数x的取值范围是[-1,5].分析 先分离出含有a,b的式子,即$\frac{1}{|b|}$(|a+b|+|a-2b|)≥f(x)恒成立,问题转化为求左式的最小值,运用绝对值不等式的性质,即可得到.
解答 解:由题意,即$\frac{1}{|b|}$(|a+b|+|a-2b|)≥f(x)恒成立,
故f(x)小于 等于$\frac{1}{|b|}$(|a+b|+|a-2b|)的最小值.
∵$\frac{1}{|b|}$(|a+b|+|a-2b|)≥$\frac{1}{|b|}$(|a+b-a+2b|)=3,
当且仅当(a+b)(a-2b)≤0时取等号,
∴$\frac{1}{|b|}$(|a+b|+|a-2b|)的最小值等于3.
∴x的范围即为不等式|x-2|≤3的解.
解不等式得-1≤x≤5.
故答案为:[-1,5].
点评 本题主要考查了不等式的恒成立问题,考查绝对值不等式的性质,通常采用分离参数的方法解决,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
3.设变量x,y满足约束条件$\left\{\begin{array}{l}{y≤0}\\{x-y+1≥0}\\{x+y-3≤0}\end{array}\right.$,则z=$\frac{x}{2}$+y的最大值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
10.对任意正数x,y,不等式$\frac{x}{3x+y}+\frac{3y}{x+3y}≤k$恒成立,则实数k的取值范围是( )
| A. | $[{\frac{5}{4},+∞})$ | B. | $[{\frac{{6-\sqrt{3}}}{4},+∞})$ | C. | [1,+∞) | D. | $[{\frac{{\sqrt{3}}}{2},+∞})$ |
20.以下是某个几何体的三视图(单位:cm),则该几何体的体积是( )
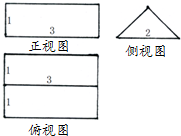

| A. | 2cm3 | B. | 3cm3 | C. | 4cm3 | D. | 5cm3 |
7.P是双曲线$\frac{x^2}{4}$-y2=1右支(在第一象限内)上的任意一点,A1,A2分别是左右顶点,O是坐标原点,直线PA1,PO,PA2的斜率分别为k1,k2,k3,则斜率之积k1k2k3的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{1}{8}$) | C. | (0,$\frac{1}{4}$) | D. | (0,$\frac{1}{2}$) |
4.对于函数f(x)=eax-lnx,(a是实常数),下列结论正确的一个是( )
| A. | a=1时,B有极大值,且极大值点(1,3) | |
| B. | a=2时,A有极小值,且极小值点x0∈(0,$\frac{1}{4}$) | |
| C. | a=$\frac{1}{2}$时,D有极小值,且极小值点x0∈(1,2) | |
| D. | a<0时,C有极大值,且极大值点x0∈(-∞,0) |
5.双曲线$\frac{x^2}{{{m^2}-4}}+\frac{y^2}{m^2}$=1(m∈Z)的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |