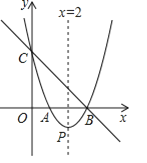题目内容
【题目】已知椭圆![]() 的长轴长为6,且椭圆
的长轴长为6,且椭圆![]() 与圆
与圆![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点P(0,1)作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
,![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形,若存在,求出点
为底边的等腰三角形,若存在,求出点![]() 的横坐标的取值范围;若不存在,请说明理由.
的横坐标的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据长轴长为6便可直接求出a的大小,然后因为椭圆和已知圆均关于x轴对称,便可得到交点坐标,然后利用待定系数法即可得到椭圆方程。
(2)设直线的方程,代入椭圆方程,利用韦达定理及中点坐标公式,求得AB中点M的坐标,利用![]() 即可求得m的表达式,利用基本不等式性质,即可求得m的取值范围。
即可求得m的表达式,利用基本不等式性质,即可求得m的取值范围。
(1)由题意可得![]() ,所以
,所以![]() .
.
由椭圆![]() 与圆
与圆![]() :
:![]() 的公共弦长为
的公共弦长为![]() ,恰为圆
,恰为圆![]() 的直径,
的直径,
可得椭圆![]() 经过点
经过点![]() ,所以
,所以![]() ,解得
,解得![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)直线![]() 的解析式为
的解析式为![]() ,设
,设![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() .假设存在点
.假设存在点
![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形,则
为底边的等腰三角形,则![]() .由
.由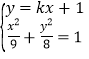 得
得![]() ,
,
故![]() ,所以
,所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() ,即
,即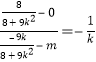 ,
,
所以![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() .
.
综上所述,在![]() 轴上存在满足题目条件的点
轴上存在满足题目条件的点![]() ,且点
,且点![]() 的横坐标的取值范围为
的横坐标的取值范围为![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】某中学对高三年级的学生进行体质测试,已知高三、一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:![]() ):
):
|
|
| 男 |
| 女 |
|
|
|
|
|
7 | 16 | 5 | 7 | 8 | 9 | 9 | ||||
9 | 8 | 17 | 1 | 8 | 4 | 5 | 2 | 9 | ||
3 | 5 | 6 | 18 | 0 | 2 | 7 | 5 | 4 | ||
1 | 2 | 4 | 19 | 0 | 1 | |||||
1 8 5 | 20 21 22 |
男生成绩不低于![]() 的定义为“合格”,成绩低于
的定义为“合格”,成绩低于![]() 的定义为“不合格”;女生成绩不低于
的定义为“不合格”;女生成绩不低于![]() 的定义为“合格”,成绩低于
的定义为“合格”,成绩低于![]() 的定义为“不合格”.
的定义为“不合格”.
(1) 求女生立定跳远成绩的中位数;
(2) 若在男生中按成绩是否合格进行分层抽样,抽取6个人,求抽取成绩“合格”的男生人数;
(3) 若从(2)问所抽取的6人中任选2人,求这2人中恰有1人成绩“合格”的概率.
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:

(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)