题目内容
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 的中点
的中点
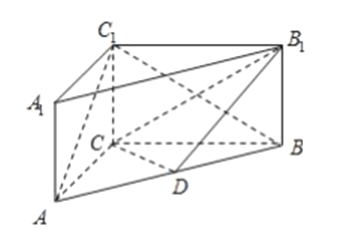
(1)证明: ![]() 平面
平面![]() ;
;
(2)在线段![]() 上找一点
上找一点![]() ,使得直线
,使得直线![]() 与
与![]() 所成角的为
所成角的为![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]()
【解析】试题分析:(1)证明线面平行,一般方法为利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找往往结合平几知识,如本题利用三角形中位线性质得线线平行,(2)研究线线角,一般可利用空间向量数量积求解,先根据题意建立恰当的空间直角坐标系,设立各点坐标,写出两直线方向向量,再根据向量数量积求夹角余弦值,最后根据线线角与向量夹角关系列关系式,求出![]() 的值.
的值.
试题解析:(Ⅰ)证明:设![]() 与
与![]() 相交于
相交于![]() ,连结
,连结![]() ,
,
![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 的中点,
的中点,
![]() ∥
∥![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,![]() ∥平面
∥平面![]()

(Ⅱ)建立空间直角坐标系, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴,
设![]()
![]() ,
, ![]()
所以![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】2017年5月13日第30届大连国际马拉松赛举行,某单位的10名跑友报名参加了半程马拉松、10公里健身跑、迷你马拉松3个项目(每人只报一项),报名情况如下:
项目 | 半程马拉松 | 10公里健身跑 | 迷你马拉松 |
人数 | 2 | 3 | 5 |
(其中:半程马拉松![]() 公里,迷你马拉松
公里,迷你马拉松![]() 公里)
公里)
(1)从10人中选出2人,求选出的两人赛程距离之差大于10公里的概率;
(2)从10人中选出2人,设![]() 为选出的两人赛程距离之和,求随机变量
为选出的两人赛程距离之和,求随机变量![]() 的分布列.
的分布列.
