题目内容
【题目】已知函数![]() (
(![]() ,
, ![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当
的图象.当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由题意,化简得到![]() ,根据相邻量对称轴间的距离求得函数的最小正周期,进而得到
,根据相邻量对称轴间的距离求得函数的最小正周期,进而得到![]() 的值,根据奇函数,求解
的值,根据奇函数,求解![]() ,得到函数的解析式,进而求解函数的单调区间即可;
,得到函数的解析式,进而求解函数的单调区间即可;
(2)根据三角函数的图象变换得到![]() 的解析式,根据题意求解
的解析式,根据题意求解![]()
的取值范围,即可求解函数的值域.
试题解析:
(1)由题意可得: ![]() ,
,
因为相邻量对称轴间的距离为![]() ,所以
,所以![]() ,
, ![]() ,
,
因为函数为奇函数,所以![]() ,
, ![]() ,
, ![]() ,
,
因为![]() ,所以
,所以![]() ,函数
,函数![]()
∵![]() ∴
∴![]()
要使![]() 单调减,需满足
单调减,需满足![]() ,
, ![]()
所以函数的减区间为![]() ;
;
(2)由题意可得: ![]()
∵![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
即函数![]() 的值域为
的值域为![]() .
.

练习册系列答案
相关题目
【题目】为贯彻落实教育部等![]() 部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行春季校园足球联赛,为迎接此次联赛,甲中学选拔了
部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行春季校园足球联赛,为迎接此次联赛,甲中学选拔了![]() 名学生组成集训队,现统计了这
名学生组成集训队,现统计了这![]() 名学生的身高,记录如下表:
名学生的身高,记录如下表:
身高 |
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
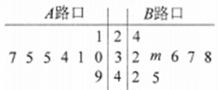
(1)请计算这![]() 名学生的身高中位数、众数,并补充完成下面的茎叶图:
名学生的身高中位数、众数,并补充完成下面的茎叶图:

(2)身高为![]() 和
和![]() 的四名学生分别为
的四名学生分别为![]() ,现从这四名学生中选
,现从这四名学生中选![]() 名担任正副门将,请利用列举法列出所有可能情况,并求学生
名担任正副门将,请利用列举法列出所有可能情况,并求学生![]() 入选正门将的概率.
入选正门将的概率.