题目内容
【题目】选修4—5：不等式选讲
已知函数f（x）＝|2x－a|＋a.
（1）若不等式f（x）≤6的解集为{x|－2≤x≤3}，求实数a的值；
（2）在（1）的条件下，若存在实数n使f（n）≤m－f（－n）成立，求实数m的取值范围．
【答案】（1） a＝1 （2）[4，＋∞）．
【解析】
试题分析：（1）根据方程的解与不等式解集关系得：－2 ，3为|2x－a|＋a =6两根，解得a＝1。也可先利用绝对值定义求不等式解集a－3≤x≤3，再根据同解得等量关系a－3＝－2 （2）不等式有解问题，一般转化为对应函数最值问题：f（n）＋f（－n） 最小值≤m，再利用绝对值定义求f（n）＋f（－n） ＝|2n－1|＋|2n＋1|＋2最小值，也可利用绝对值三角不等式求最小值：|2n－1|＋|2n＋1|
试题解析：（1）由|2x－a|＋a≤6，得|2x－a|≤6－a，
∴a－6≤2x－a≤6－a，即a－3≤x≤3，∴a－3＝－2，∴a＝1
（2）由（1）知f（x）＝|2x－1|＋1，
令φ（n）＝f（n）＋f（－n），
则φ（n）＝|2n－1|＋|2n＋1|＋2
＝
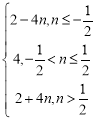
∴φ（n）的最小值为4，故实数m的取值范围是[4，＋∞）．
名校课堂系列答案
【题目】某初级中学有三个年级，各年级男、女生人数如下表：
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 | z | 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.
（1）求z的值；
（2）用分层抽样的方法在初三年级中抽取一个容量为5的样本，将该样本看成一个总体,从中任选2名学生，求至少有1名女生的概率；
（3）用随机抽样的方法从初二年级女生中选出8人，测量它们的左眼视力，结果如下：1.2, 1.5, 1.2, 1.5, 1.5, 1.3, 1.0, 1.2.把这8人的左眼视力看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0.1的概率.
【题目】关于某设备的使用年限
和所支出的维修费用
（万元），有如下的统计资料：
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)如由资料可知
对
呈线形相关关系.试求：线形回归方程；（
，
）
(2)估计使用年限为10年时，维修费用是多少？
