题目内容
数列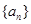 的前n项和为Sn
的前n项和为Sn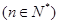 ,点(an,Sn)在直线y=2x-3n上.
,点(an,Sn)在直线y=2x-3n上.
(1)若数列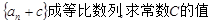 ;
;
(2)求数列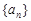 的通项公式;
的通项公式;
(3)数列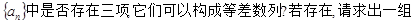 适合条件的项;若不存在,请说明理由.
适合条件的项;若不存在,请说明理由.
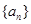 的前n项和为Sn
的前n项和为Sn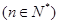 ,点(an,Sn)在直线y=2x-3n上.
,点(an,Sn)在直线y=2x-3n上.(1)若数列
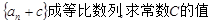 ;
;(2)求数列
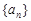 的通项公式;
的通项公式;(3)数列
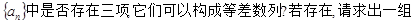 适合条件的项;若不存在,请说明理由.
适合条件的项;若不存在,请说明理由. (1) (2)
(2) (3)见解析
(3)见解析
 (2)
(2) (3)见解析
(3)见解析(1)
得 ,
,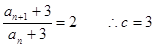 .
.
(2)在(1)的基础上可求出 ,进而求出
,进而求出 .
.
(3) 设存在S,P,r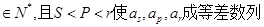 ,
,
 然后利用
然后利用 ,建立p,s,r的关系式.再分析式子结构及s、p、r的取值,看等式是否成立.从而确定是否存在
,建立p,s,r的关系式.再分析式子结构及s、p、r的取值,看等式是否成立.从而确定是否存在
(1)由题意知 ,(1分)
,(1分)
得 ,(3分)∴
,(3分)∴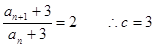 (5分)
(5分)
(2)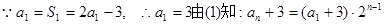 (6分)
(6分)
 (8分)
(8分)
(3)设存在S,P,r ,(9分)
,(9分)
 (10分)
(10分)
即
 (*) (12分)
(*) (12分)
因为s、p、r 为偶数
为偶数
1+2 ,(*)式产生矛盾.所以这样的三项不存在
,(*)式产生矛盾.所以这样的三项不存在

得
 ,
,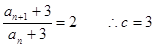 .
.(2)在(1)的基础上可求出
 ,进而求出
,进而求出 .
.(3) 设存在S,P,r
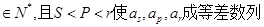 ,
, 然后利用
然后利用 ,建立p,s,r的关系式.再分析式子结构及s、p、r的取值,看等式是否成立.从而确定是否存在
,建立p,s,r的关系式.再分析式子结构及s、p、r的取值,看等式是否成立.从而确定是否存在(1)由题意知
 ,(1分)
,(1分)得
 ,(3分)∴
,(3分)∴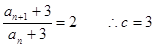 (5分)
(5分) (2)
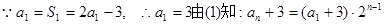 (6分)
(6分) (8分)
(8分) (3)设存在S,P,r
 ,(9分)
,(9分) (10分)
(10分) 即

 (*) (12分)
(*) (12分) 因为s、p、r
 为偶数
为偶数1+2
 ,(*)式产生矛盾.所以这样的三项不存在
,(*)式产生矛盾.所以这样的三项不存在
练习册系列答案
相关题目
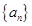 中,
中, 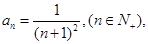 记
记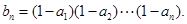
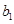 、
、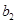 、
、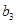 、
、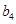 并推测
并推测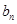 ;
;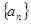 中,
中,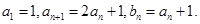
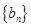 是等比数列;
是等比数列;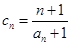 ,求数列
,求数列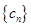 的前
的前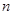 项和
项和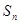

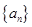 的前n项和为
的前n项和为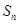 ,若
,若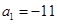 ,
,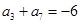 ,则当
,则当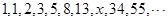 中的
中的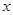 的值为 ▲ .
的值为 ▲ . }前n项和为
}前n项和为 ,
, ,则
,则 ______.
______.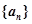 的各项均为正数,
的各项均为正数,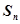 为其前
为其前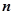 项和,对于任意
项和,对于任意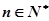 ,总有
,总有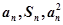 成等差数列.设数列
成等差数列.设数列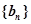 的前
的前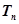 ,且
,且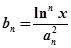 ,则对任意实数
,则对任意实数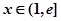 (
(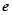 是常数,
是常数,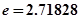 )和任意正整数
)和任意正整数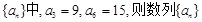 的公差
的公差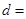




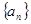 是等差数列,首项
是等差数列,首项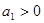 ,且
,且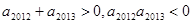 ,则使前n项和Sn>0成立的最大自然数n是( )
,则使前n项和Sn>0成立的最大自然数n是( )