题目内容
【题目】某高中数学建模兴趣小组的同学为了研究所在地区男高中生的身高与体重的关系,从若干个高中男学生中抽取了1000个样本,得到如下数据.
数据一:身高在![]() (单位:
(单位:![]() )的体重频数统计
)的体重频数统计
体重 ( |
|
|
|
|
|
|
|
|
人数 | 20 | 60 | 100 | 100 | 80 | 20 | 10 | 10 |
数据二:身高所在的区间含样本的个数及部分数据
身高 |
|
|
|
|
|
平均体重
| 45 | 53.6 | 60 | 75 |
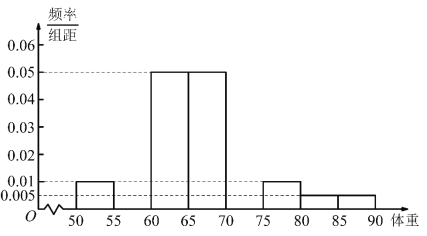
(1)依据数据一将上面男高中生身高在![]() (单位:
(单位:![]() )体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在
)体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在![]() (单位:
(单位:![]() )的中学生的平均体重;(保留小数点后一位)
)的中学生的平均体重;(保留小数点后一位)
(2)依据数据一、二,计算身高(取值为区间中点)和体重的相关系数约为0.99,能否用线性回归直线来刻画中学生身高与体重的相关关系,请说明理由;若能,求出该回归直线方程;
(3)说明残差平方和或相关指数![]() 与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)
与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)
参考公式: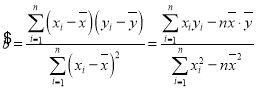 ,
,![]() .
.
参考数据:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ;(4)
;(4)![]() .
.
【答案】(1)答案见解析,![]()
![]() ;(2)能;因为
;(2)能;因为![]() ,线性相关很强,故可以用线性回归直线来刻画中学生身高与体重的相关;
,线性相关很强,故可以用线性回归直线来刻画中学生身高与体重的相关;![]() ;(3)残差平方和越小或相关指数
;(3)残差平方和越小或相关指数![]() 越接近于1,线性回归模型拟合效果越好.
越接近于1,线性回归模型拟合效果越好.
【解析】
(1)计算总人数得到频率,补充频率直方图并计算平均值得到答案.
(2)根据![]() 得到线性相关很强,再利用回归方程公式计算得到答案.
得到线性相关很强,再利用回归方程公式计算得到答案.
(3)直接根据残差平方和或相关指数![]() 的定义得到答案.
的定义得到答案.
(1)身高在![]() 的总人数为:
的总人数为:![]() ,
,
体重在![]() 的频率为:
的频率为:![]() ,体重在
,体重在![]() 的频率为:
的频率为:![]() ,
,
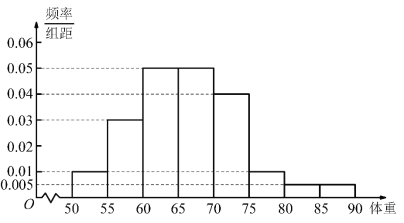
平均体重为:
![]()
![]() .
.
(2)因为![]() ,线性相关很强,故可以用线性回归直线来刻画中学生身高与体重的相关,
,线性相关很强,故可以用线性回归直线来刻画中学生身高与体重的相关,
![]() ,
,![]() ,
,
 ,
,
![]() ,
,
所以回归直线方程为:![]() .
.
(3)残差平方和越小或相关指数![]() 越接近于1,线性回归模型拟合效果越好.
越接近于1,线性回归模型拟合效果越好.

【题目】辽宁省六校协作体(葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中)中的某校文科实验班的![]() 名学生期中考试的语文、数学成绩都不低于
名学生期中考试的语文、数学成绩都不低于![]() 分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:
分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
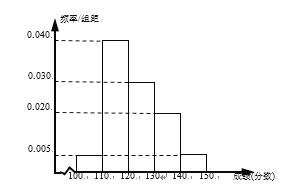
(1)根据频率分布直方图,估计这![]() 名学生语文成绩的中位数和平均数;(同一组数据用该区间的中点值作代表;中位数精确到
名学生语文成绩的中位数和平均数;(同一组数据用该区间的中点值作代表;中位数精确到![]() )
)
(2)若这![]() 名学生语文成绩某些分数段的人数
名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 |
|
|
|
|
|
|
|
|
|
从数学成绩在![]() 的学生中随机选取
的学生中随机选取![]() 人,求选出的
人,求选出的![]() 人中恰好有
人中恰好有![]() 人数学成绩在
人数学成绩在![]() 的概率.
的概率.
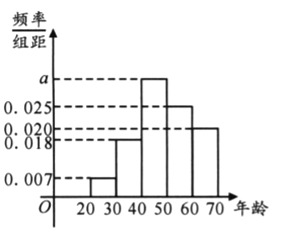
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
年龄 (单位:岁) |
|
|
|
|
|
保费 (单位:元) |
|
|
|
|
|
(1)用样本的频率分布估计总体分布,为使公司不亏本,求![]() 精确到整数时的最小值
精确到整数时的最小值![]() ;
;
(2)经调查,年龄在![]() 之间老人每
之间老人每![]() 人中有
人中有![]() 人患该项疾病(以此频率作为概率).该病的治疗费为
人患该项疾病(以此频率作为概率).该病的治疗费为![]() 元,如果参保,保险公司补贴治疗费
元,如果参保,保险公司补贴治疗费![]() 元.某老人年龄
元.某老人年龄![]() 岁,若购买该项保险(
岁,若购买该项保险(![]() 取
取![]() 中的
中的![]() ).针对此疾病所支付的费用为
).针对此疾病所支付的费用为![]() 元;若没有购买该项保险,针对此疾病所支付的费用为
元;若没有购买该项保险,针对此疾病所支付的费用为![]() 元.试比较
元.试比较![]() 和
和![]() 的期望值大小,并判断该老人购买此项保险是否划算?
的期望值大小,并判断该老人购买此项保险是否划算?
【题目】“地摊经济”是李克强总理在本届政府工作报告中向全国人民发出的口号,某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() (
(![]() ,2,3,4,5,6),如表所示:
,2,3,4,5,6),如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y(件) | q | 84 | 83 | 80 | 75 | 68 |
已知![]() ,
,![]() ,
,![]()
(1)试求q,若变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数
称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式:线性回归方程中![]() ,
,![]() 的最小二乘估计分别为
的最小二乘估计分别为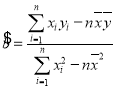 ,
,![]() )
)