题目内容
已知:函数f(x)=|x-a|,g(x)=x2-2ax+1,若f(0)=g(0).
(1)求正实数a的取值;
(2)求函数h(x)=g(x)-f(x)的解析式(用分段函数表示);
(3)画出函数h(x)的简图,并写出函数的值域和单调递增区间.
(1)求正实数a的取值;
(2)求函数h(x)=g(x)-f(x)的解析式(用分段函数表示);
(3)画出函数h(x)的简图,并写出函数的值域和单调递增区间.

(1)f(0)=|0-a|=|a|=a,
g(0)=0-0+1=1,
因为f(0)=g(0),
所以a=1.
(2)f(x)-g(x)=|x-1|-x2+2x-1,
当x≥1时,f(x)-g(x)=(x-1)-x2+2x-1=-x2+3x-2,
当x<1时,f(x)-g(x)=(1-x)-x2+2x-1=-x2+x,
∴h(x)=g(x)-f(x)=
.
(3)当x≥1时,y=h(x)=-x2+3x-2的图象的对称轴是x=
,
顶点坐标是(
,
),
与x轴交于点(1,0)和(2,0);
当x<1时,y=h(x)=-x2+x的图象的对称轴是x=
,
顶点坐标是(
,
),
与x轴交于点(0,0)和(1,0).
结合抛物线的对称性,
作出h(x)=
的简图如下:
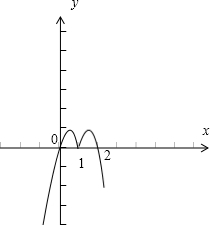
结合图象,知函数的值域为(-∞,
],
单调递增区间为(-∞,
]∪[1,
].
g(0)=0-0+1=1,
因为f(0)=g(0),
所以a=1.
(2)f(x)-g(x)=|x-1|-x2+2x-1,
当x≥1时,f(x)-g(x)=(x-1)-x2+2x-1=-x2+3x-2,
当x<1时,f(x)-g(x)=(1-x)-x2+2x-1=-x2+x,
∴h(x)=g(x)-f(x)=
|
(3)当x≥1时,y=h(x)=-x2+3x-2的图象的对称轴是x=
| 3 |
| 2 |
顶点坐标是(
| 3 |
| 2 |
| 1 |
| 4 |
与x轴交于点(1,0)和(2,0);
当x<1时,y=h(x)=-x2+x的图象的对称轴是x=
| 1 |
| 2 |
顶点坐标是(
| 1 |
| 2 |
| 1 |
| 4 |
与x轴交于点(0,0)和(1,0).
结合抛物线的对称性,
作出h(x)=
|

结合图象,知函数的值域为(-∞,
| 1 |
| 4 |
单调递增区间为(-∞,
| 1 |
| 2 |
| 3 |
| 2 |

练习册系列答案
相关题目
 满足
满足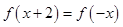 ,且当
,且当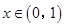 时,
时,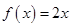 ,则
,则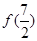 的值为 .
的值为 .