题目内容
若数列{an}满足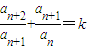 (k为常数),则称数列{an}为等比和数列,k称为公比和.已知数列{an}是以3为公比和的等比和数列,其中a1=1,a2=2,则a2009= .
(k为常数),则称数列{an}为等比和数列,k称为公比和.已知数列{an}是以3为公比和的等比和数列,其中a1=1,a2=2,则a2009= .
【答案】分析:由n=1,2,3,4,5,6,分别求出a1,a2,a3,a4,a5,a6,a7,a8,然后总结规律,求出a2009.
解答:解: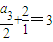 ,a3=2,
,a3=2,
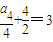 ,a4=4,
,a4=4,
∴a3=a4=22.
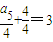 ,a5=8,
,a5=8,
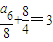 ,a6=8,
,a6=8,
∴a5=a6=23,
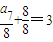 ,a7=16.
,a7=16.
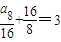 ,a8=16.
,a8=16.
∴a7=a8=24.
由此可知a2008=a2009=21004.
故答案为:21004.
点评:本题考查数列的递推式,解题时要认真审题,总结规律,仔细求解.
解答:解:
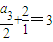 ,a3=2,
,a3=2,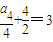 ,a4=4,
,a4=4,∴a3=a4=22.
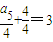 ,a5=8,
,a5=8,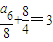 ,a6=8,
,a6=8,∴a5=a6=23,
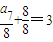 ,a7=16.
,a7=16.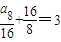 ,a8=16.
,a8=16.∴a7=a8=24.
由此可知a2008=a2009=21004.
故答案为:21004.
点评:本题考查数列的递推式,解题时要认真审题,总结规律,仔细求解.

练习册系列答案
相关题目