题目内容
7．
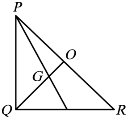如图，△PQR中，∠Q=90°，又∠QPR=45°，已知G为△PQR的重心，若OG=a，求△PQR的周长（用a表示）．
分析 利用三角形重心的性质，结合等腰直角三角形的性质，即可得出结论．
解答 解：由题意，OQ⊥PR，OQ=3a，
∴PR=6a，
∴△PQR的周长为6a+2×$\frac{\sqrt{2}}{2}$×6a=6（1+$\sqrt{2}$）a．
点评 本题考查三角形重心的性质，等腰直角三角形的性质，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
17．下列命题中，真命题的是（ ）
| A． | ?x0∈R，${e^{x_0}}$＜0 | |
| B． | 函数$f（x）={x^2}-{log_{\frac{1}{2}}}$x的零点个数为2 | |
| C． | 若p∨q为真命题，则p∧q也为真命题 | |
| D． | 命题“若m＞0，则方程x2+x-m=0有实数根”的逆否命题为：“若方程x2+x-m=0无实数根，则m≤0” |